如图,在 中, , ,点C是 的中点,以OC为半径作 .
(1)求证: 是 的切线;
(2)若 ,求 的长.

点 是平行四边形 的对角线 所在直线上的一个动点(点 不与点 、 重合),分别过点 、 向直线 作垂线,垂足分别为点 、 .点 为 的中点.
(1)如图1,当点 与点 重合时,线段 和 的关系是 ;
(2)当点 运动到如图2所示的位置时,请在图中补全图形并通过证明判断(1)中的结论是否仍然成立?
(3)如图3,点 在线段 的延长线上运动,当 时,试探究线段 、 、 之间的关系.

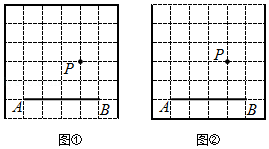
如图,在方格纸中,点 , , 都在格点上.请按要求画出以 为边的格点四边形,使 在四边形内部(不包括边界上),且 到四边形的两个顶点的距离相等.
(1)在图甲中画出一个 .
(2)在图乙中画出一个四边形 ,使 ,且 .(注:图甲、乙在答题纸上)
如图,点 在矩形 的对角线 上,且不与点 , 重合,过点 分别作边 , 的平行线,交两组对边于点 , 和 , .
(1)求证: ;
(2)证明四边形 和四边形 都是矩形,并直接写出它们面积之间的关系.

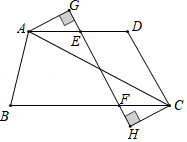
如图,四边形 中, ,点 、 分别在 、 上, ,过点 、 分别作 的垂线,垂足为 、 .
(1)求证: ;
(2)连接 ,线段 与 是否互相平分?请说明理由.
如图, 为圆 的直径, 为圆 上一点, 为 延长线一点,且 , 于点 .
(1)求证:直线 为圆 的切线;
(2)设 与圆 交于点 , 的延长线与 交于点 ,已知 , , ,求 的值.

数学课上,张老师举了下面的例题:
例1 等腰三角形 中, ,求 的度数.(答案:
例2 等腰三角形 中, ,求 的度数,(答案: 或 或
张老师启发同学们进行变式,小敏编了如下一题:
变式 等腰三角形 中, ,求 的度数.
(1)请你解答以上的变式题.
(2)解(1)后,小敏发现, 的度数不同,得到 的度数的个数也可能不同,如果在等腰三角形 中,设 ,当 有三个不同的度数时,请你探索 的取值范围.
我们定义:有一组邻角相等的凸四边形叫做“等邻角四边形”
(1)概念理解:
请你根据上述定义举一个等邻角四边形的例子;
(2)问题探究:
如图1,在等邻角四边形 中, , , 的中垂线恰好交于 边上一点 ,连接 , ,试探究 与 的数量关系,并说明理由;
(3)应用拓展:
如图2,在 与 中, , , ,将 绕着点 顺时针旋转角 得到 △ (如图 ,当凸四边形 为等邻角四边形时,求出它的面积.

如图,以 的直角边 为直径作 交斜边 于点 ,过圆心 作 ,交 于点 ,连接 .
(1)判断 与 的位置关系并说明理由;
(2)求证: ;
(3)若 , ,求 的长.

如图, 是 的直径,过点 作 的切线 ,点 是射线 上的动点,连接 ,过点 作 ,交 于点 ,连接 .
(1)求证: 是 的切线;
(2)当四边形 是平行四边形时,求 的度数.

如图,在 中, , , 是 边上一点(点 与 , 不重合),连接 ,将线段 绕点 按逆时针方向旋转 得到线段 ,连接 交 于点 ,连接 .
(1)求证: ;
(2)当 时,求 的度数.

如图,在 中, ,以 为直径的半圆 交 于点 ,过点 作半圆 的切线,交 于点 .
(1)求证: ;
(2)若 , ,求 的长.
