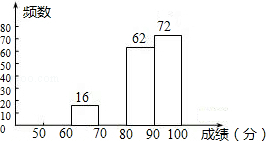
某区八年级有3000名学生参加“爱我中华知识竞赛”活动.为了了解本次知识竞赛的成绩分布情况,从中抽取了200名学生的得分进行统计.
成绩x
|
频数
|
频率
|
50≤x<60
|
10
|
|
60≤x<70
|
16
|
0.08
|
70≤x<80
|
|
0.02
|
80≤x<90
|
62
|
|
90≤x<100
|
72
|
0.36
|
请你根据不完整的表格,回答下列问题:
(1)补全频率分布直方图;
(2)若将得分转化为等级,规定50≤x<60评为“D”,60≤x<70评为“C”,70≤x<90评为“B”,90≤x<100评为“A”.这次全区八年级参加竞赛的学生约有多少学生参赛成绩被评为“D”?如果随机抽查一名参赛学生的成绩等级,则这名学生的成绩等级哪一个等级的可能性大?请说明理由.