2022年重庆市中考数学试卷(a卷)
如图,直线AB,CD被直线CE所截, , ,则 的度数为( )

| A. |
40° |
B. |
50° |
C. |
130° |
D. |
150° |
如图,曲线表示一只蝴蝶在飞行过程中离地面的高度h(m)随飞行时间t(s)的变化情况,则这只蝴蝶飞行的最高高度约为( )
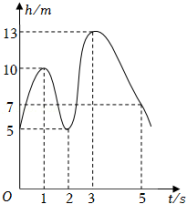
| A. |
5m |
B. |
7m |
C. |
10m |
D. |
13m |
如图,△ABC与△DEF位似,点O为位似中心,相似比为 .若△ABC的周长为4,则△DEF的周长是( )

| A. |
4 |
B. |
6 |
C. |
9 |
D. |
16 |
用正方形按如图所示的规律拼图案,其中第①个图案中有5个正方形,第②个图案中有9个正方形,第③个图案中有13个正方形,第④个图案中有17个正方形,此规律排列下去,则第⑨个图案中正方形的个数为( )

| A. |
32 |
B. |
34 |
C. |
37 |
D. |
41 |
小区新增了一家快递店,第一天揽件200件,第三天揽件242件,设该快递店揽件日平均增长率为 ,根据题意,下面所列方程正确的是( )
| A. |
|
B. |
|
| C. |
|
D. |
|
如图,在正方形ABCD中,AE平分∠BAC交BC于点E,点F是边AB上一点,连接DF,若 ,则∠CDF的度数为( )
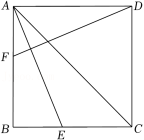
| A. |
45° |
B. |
60° |
C. |
67.5° |
D. |
77.5° |
如图,AB是 的切线,B为切点,连接AO交 于点C,延长AO交 于点D,连接BD.若 ,且 ,则AB的长度是( )
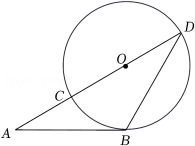
| A. |
3 |
B. |
4 |
C. |
|
D. |
|
若关于 的一元一次不等式组 的解集为 ,且关于 的分式方程 的解是负整数,则所有满足条件的整数 的值之和是( )
| A. |
﹣26 |
B. |
﹣24 |
C. |
﹣15 |
D. |
﹣13 |
在多项式 中任意加括号,加括号后仍只有减法运算,然后按给出的运算顺序重新运算,称此为“加算操作”.例如: , ,….
下列说法:
①至少存在一种“加算操作”,使其运算结果与原多项式相等;
②不存在任何“加算操作”,使其运算结果与原多项式之和为0;
③所有可能的“加算操作”共有8种不同运算结果.
其中正确的个数是( )
| A. |
0 |
B. |
1 |
C. |
2 |
D. |
3 |
有三张完全一样正面分别写有字母A,B,C的卡片.将其背面朝上并洗匀,从中随机抽取一张,记下卡片上的字母后放回洗匀,再从中随机抽取一张,则抽取的两张卡片上的字母相同的概率是 .
如图,菱形ABCD中,分别以点A,C为圆心,AD,CB长为半径画弧,分别交对角线AC于点E,F.若 , ,则图中阴影部分的面积为 .(结果不取近似值)

为进一步改善生态环境,村委会决定在甲、乙、丙三座山上种植香樟和红枫.初步预算,这三座山各需两种树木数量和之比为 ,需香樟数量之比为 ,并且甲、乙两山需红枫数量之比为 .在实际购买时,香樟的价格比预算低20%,红枫的价格比预算高25%,香樟购买数量减少了6.25%,结果发现所花费用恰好与预算费用相等,则实际购买香樟的总费用与实际购买红枫的总费用之比为 .
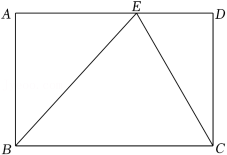
在学习矩形的过程中,小明遇到了一个问题:在矩形ABCD中,E是AD边上的一点,试说明△BCE的面积与矩形ABCD的面积之间的关系.他的思路是:首先过点E作BC的垂线,将其转化为证明三角形全等,然后根据全等三角形的面积相等使问题得到解决.请根据小明的思路完成下面的作图与填空:
证明:用直尺和圆规,过点E作BC的垂线EF,垂足为F(只保留作图痕迹).
在△BAE和△EFB中,
∵EF⊥BC,
∴∠EFB=90°.
又∠A=90°,
∴ ①
∵AD∥BC,
∴ ②
又 ③
∴△BAE≌△EFB(AAS).
同理可得 ④
∴ .
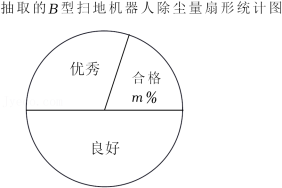
公司生产A、B两种型号的扫地机器人,为了解它们的扫地质量,工作人员从某月生产的A、B型扫地机器人中各随机抽取10台,在完全相同条件下试验,记录下它们的除尘量的数据(单位:g),并进行整理、描述和分析(除尘量用 表示,共分为三个等级:合格 ,良好 ,优秀 ),下面给出了部分信息:
10台A型扫地机器人的除尘量:83,84,84,88,89,89,95,95,95,98.
10台B型扫地机器人中“良好”等级包含的所有数据为:85,90,90,90,94
抽取的A、B型扫地机器人除尘量统计表
|
型号 |
平均数 |
中位数 |
众数 |
方差 |
“优秀”等级所占百分比 |
|
A |
90 |
89 |
a |
26.6 |
40% |
|
B |
90 |
b |
90 |
30 |
30% |
根据以上信息,解答下列问题:
(1)填空:a= ,b= ,m= ;
(2)这个月公司可生产B型扫地机器人共3000台,估计该月B型扫地机器人“优秀”等级的台数;
(3)根据以上数据,你认为该公司生产的哪种型号的扫地机器人扫地质量更好?请说明理由(写出一条理由即可).
已知一次函数 的图象与反比例函数 的图象相交于点 , .
(1)求一次函数的表达式,并在图中画出这个一次函数的图象;
(2)根据函数图象,直接写出不等式 的解集;
(3)若点C是点B关于y轴的对称点,连接AC,BC,求△ABC的面积.

在全民健身运动中,骑行运动颇受市民青睐,甲、乙两骑行爱好者约定从A地沿相同路线骑行去距A地30千米的B地,已知甲骑行的速度是乙的1.2倍.
(1)若乙先骑行2千米,甲才开始从A地出发,则甲出发半小时恰好追上乙,求甲骑行的速度;
(2)若乙先骑行20分钟,甲才开始从A地出发,则甲、乙恰好同时到达B地,求甲骑行的速度.
如图,三角形花园ABC紧邻湖泊,四边形ABDE是沿湖泊修建的人行步道.经测量,点C在点A的正东方向, .点E在点A的正北方向.点B,D在点C的正北方向, .点B在点A的北偏东30°,点D在点E的北偏东45°.
(1)求步道DE的长度(精确到个位);
(2)点D处有直饮水,小红从A出发沿人行步道去取水,可以经过点B到达点D,也可以经过点E到达点D.请计算说明他走哪一条路较近?
(参考数据: , )

若一个四位数M的个位数字与十位数字的平方和恰好是M去掉个位与十位数字后得到的两位数,则这个四位数M为“勾股和数”.
例如: ,∵ ,∴2543是“勾股和数”;
又如: ,∵ , ,∴4325不是“勾股和数”.
(1)判断2022,5055是否是“勾股和数”,并说明理由;
(2)一个“勾股和数”M的千位数字为a,百位数字为b,十位数字为c,个位数字为d,记 , .当 , 均是整数时,求出所有满足条件的M.
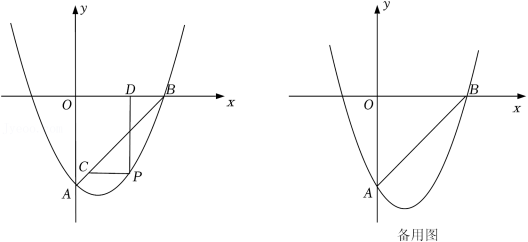
如图,在平面直角坐标系中,抛物线 与直线AB交于点 , .
(1)求该抛物线的函数表达式;
(2)点P是直线AB下方抛物线上的一动点,过点P作 轴的平行线交AB于点C,过点P作 轴的平行线交 轴于点D,求 的最大值及此时点P的坐标;
(3)在(2)中 取得最大值的条件下,将该抛物线沿水平方向向左平移5个单位,点E为点P的对应点,平移后的抛物线与 轴交于点F,M为平移后的抛物线的对称轴上一点.在平移后的抛物线上确定一点N,使得以点E,F,M,N为顶点的四边形是平行四边形,写出所有符合条件的点N的坐标,并写出求解点N的坐标的其中一种情况的过程.
如图,在锐角△ABC中, ,点D,E分别是边AB,AC上一动点,连接BE交直线CD于点F.
(1)如图1,若 ,且 , ,求 的度数;
(2)如图2,若 ,且 ,在平面内将线段AC绕点C顺时针方向旋转60°得到线段CM,连接MF,点N是MF的中点,连接CN.在点D,E运动过程中,猜想线段BF,CF,CN之间存在的数量关系,并证明你的猜想;
(3)若 ,且 ,将 沿直线AB翻折至 所在平面内得到 ,点H是AP的中点,点K是线段PF上一点,将 沿直线HK翻折至 所在平面内得到 ,连接PQ.在点D,E运动过程中,当线段PF取得最小值,且 时,请直接写出 的值.





 粤公网安备 44130202000953号
粤公网安备 44130202000953号