2022年贵州省铜仁市中考数学试卷
2022年4月18日,国家统计局发布数据,今年一季度国内生产总值 亿元.同比增长 ,比2021年四季度环比增长 .把 用科学记数法表示为( )
| A. |
|
B. |
|
| C. |
|
D. |
|
在一个不透明的布袋内,有红球 个,黄球 个,白球 个,蓝球 个,它们除颜色外,大小、质地都相同.若随机从袋中摸取一个球,则摸中哪种球的概率最大( )
| A. |
红球 |
B. |
黄球 |
C. |
白球 |
D. |
蓝球 |
为了增强学生的安全防范意识,某校初三(1)班班委举行了一次安全知识抢答赛,抢答题一共 个,记分规则如下:每答对一个得 分,每答错或不答一个扣 分.小红一共得 分,则小红答对的个数为( )
| A. |
|
B. |
|
C. |
|
D. |
|
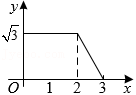
如图,等边 、等边 的边长分别为 和 .开始时点 与点 重合, 在 上, 在 上, 沿 向右平移,当点 到达点 时停止.在此过程中,设 重合部分的面积为 , 移动的距离为 ,则 与 的函数图象大致为( )
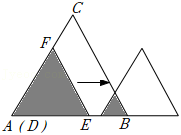
| A. |
|
B. |
|
| C. |
|
D. |
|
如图,四边形 为菱形, ,延长 到 ,在 内作射线 ,使得 ,过点 作 ,垂足为 .若 ,则 的长为_____(结果保留根号).

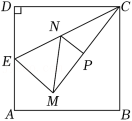
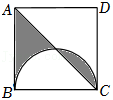
如图,在边长为 的正方形 中,点 为 的中点,将 沿 翻折得 ,点 落在四边形 内.点 为线段 上的动点,过点 作 交 于点 ,则 的最小值为_____.
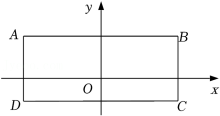
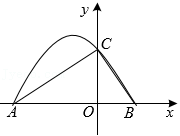
在平面直角坐标系内有三点 .
(1)求过其中两点的直线的函数表达式(选一种情形作答);
(2)判断 三点是否在同一直线上,并说明理由.
2021年7月,中共中央办公厅,国务院办公厅印发了《关于进一步减轻义务教育阶段学生作业负担和校外培训负担的意见》.某中学为了切实减轻学生作业负担,落实课后服务相关要求,开设了书法、摄影、篮球、足球、乒乓球五项课后服务活动,为了解学生的个性化需求,学校随机抽取了部分学生进行问卷调查,并将调查结果绘制成如图所示的扇形统计图和条形统计图,请你根据给出的信息解答下列问题:

(1)求 的值并把条形统计图补充完整;
(2)若该校有 名学生,试估计该校参加“书法”活动的学生有多少人?
(3)结合调查信息,请你给该校课后服务活动项目开设方面提出一条合理化的建议.
科学规范戴口罩是阻断新冠病毒传播的有效措施之一,某口罩生产厂家接到一公司的订单,生产一段时间后,还剩 万个口罩未生产,厂家因更换设备,生产效率比更换设备前提高了 .结果刚好提前 天完成订单任务.求该厂家更换设备前和更换设备后每天各生产多少万个口罩?
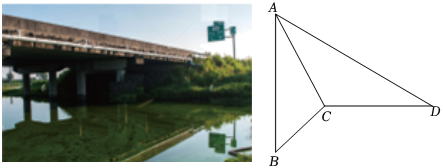
为了测量高速公路某桥的桥墩高度,某数学兴趣小组在同一水平地面 两处实地测量,如图所示.在 处测得桥墩顶部 处的仰角为 和桥墩底部 处的俯角为 ,在 处测得桥墩顶部 处的仰角为 ,测得 两点之间的距离为 ,直线 在同一平面内,请你用以上数据,计算桥墩 的高度.(结果保留整数,参考数据: , )
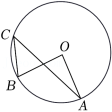
如图, 是以 为直径的 上一点,过点 的切线 交 的延长线于点 ,过点 作 交 的延长线于点 ,垂足为点 .
(1)求证: ;
(2)若 , ,求 的长.

为实施“乡村振兴”计划,某村产业合作社种植了“千亩桃园”.2022年该村桃子丰收,销售前对本地市场进行调查发现:当批发价为 千元/吨时,每天可售出 吨,每吨涨 千元,每天销量将减少 吨,据测算,每吨平均投入成本 千元,为了抢占市场,薄利多销,该村产业合作社决定,批发价每吨不低于 千元,不高于 千元.请解答以下问题:
(1)求每天销量 (吨)与批发价 (千元/吨)之间的函数关系式,并直接写出自变量 的取值范围;
(2)当批发价定为多少时,每天所获利润最大?最大利润是多少?





 粤公网安备 44130202000953号
粤公网安备 44130202000953号