初中数学三角形解答题

如图， $\mathit{PA}$是以 $\mathit{AC}$为直径的 $\odot O$的切线，切点为 $A$，过点 $A$作 $\mathit{AB}\perp \mathit{OP}$，交 $\odot O$于点 $B$．

（1）求证： $\mathit{PB}$是 $\odot O$的切线；

（2）若 $\mathit{AB}=6$， $\cos \angle \mathit{PAB}=\frac{3}{5}$，求 $\mathit{PO}$的长．

如图，点 $E$是正方形 $\mathit{ABCD}$的边 $\mathit{BC}$上的动点， $\angle \mathit{AEF}=90°$，且 $\mathit{EF}=\mathit{AE}$， $\mathit{FH}\perp \mathit{BH}$．

（1）求证： $\mathit{BE}=\mathit{CH}$；

（2）若 $\mathit{AB}=3$， $\mathit{BE}=x$，用 $x$表示 $\mathit{DF}$的长．

（1）如图，已知 $\mathit{\Delta ABC}$， $P$为边 $\mathit{AB}$上一点，请用尺规作图的方法在边 $\mathit{AC}$上求作一点 $E$，使 $\mathit{AE}+\mathit{EP}=\mathit{AC}$．（保留作图痕迹，不写作法）

（2）在图中，如果 $\mathit{AC}=6\mathit{cm}$， $\mathit{AP}=3\mathit{cm}$，则 $\mathit{\Delta APE}$的周长是 　　 $\mathit{cm}$．

如图，在矩形 $\mathit{ABCD}$中，点 $M$在 $\mathit{DC}$上， $\mathit{AM}=\mathit{AB}$，且 $\mathit{BN}\perp \mathit{AM}$，垂足为 $N$．

（1）求证： $\mathit{\Delta ABN}\cong \mathit{\Delta MAD}$；

（2）若 $\mathit{AD}=2$， $\mathit{AN}=4$，求四边形 $\mathit{BCMN}$的面积．

如图，在 $\mathit{\Delta ABC}$中， $\angle B=40°$， $\angle C=50°$．

（1）通过观察尺规作图的痕迹，可以发现直线 $\mathit{DF}$是线段 $\mathit{AB}$的 　　，射线 $\mathit{AE}$是 $\angle \mathit{DAC}$的 　　；

（2）在（1）所作的图中，求 $\angle \mathit{DAE}$的度数．

如图， $\odot O$与等边 $\mathit{\Delta ABC}$的边 $\mathit{AC}$， $\mathit{AB}$分别交于点 $D$， $E$， $\mathit{AE}$是直径，过点 $D$作 $\mathit{DF}\perp \mathit{BC}$于点 $F$．

（1）求证： $\mathit{DF}$是 $\odot O$的切线；

（2）连接 $\mathit{EF}$，当 $\mathit{EF}$是 $\odot O$的切线时，求 $\odot O$的半径 $r$与等边 $\mathit{\Delta ABC}$的边长 $a$之间的数量关系．

如图， $D$是 $\mathit{\Delta ABC}$的边 $\mathit{AB}$上一点， $\mathit{CF}//\mathit{AB}$， $\mathit{DF}$交 $\mathit{AC}$于 $E$点， $\mathit{DE}=\mathit{EF}$．

（1）求证： $\mathit{\Delta ADE}\cong \mathit{\Delta CFE}$；

（2）若 $\mathit{AB}=5$， $\mathit{CF}=4$，求 $\mathit{BD}$的长．

如图，有一池塘，要测池塘两端 $A$、 $B$的距离，可先在平地上取一个点 $C$，从点 $C$不经过池塘可以直接到达点 $A$和 $B$，连接 $\mathit{AC}$并延长到点 $D$，使 $\mathit{CD}=\mathit{CA}$，连接 $\mathit{BC}$并延长到点 $E$，使 $\mathit{CE}=\mathit{CB}$，连接 $\mathit{DE}$，那么量出 $\mathit{DE}$的长就是 $A$、 $B$的距离，为什么？请结合解题过程，完成本题的证明．

证明：在 $\mathit{\Delta DEC}$和 $\mathit{\Delta ABC}$中，

$\left\{\begin{array}{c}\mathit{CD}=(??)\\ (??)\\ \mathit{CE}=(??)\end{array}\right.$，

$\therefore \mathit{\Delta DEC}\cong \mathit{\Delta ABC}\left(\mathit{SAS}\right)$，

$\therefore$　 $\mathit{DE}=\mathit{AB}$　．

如图， $\mathit{BD}$为 $▱\mathit{ABCD}$的对角线．

（1）作对角线 $\mathit{BD}$的垂直平分线，分别交 $\mathit{AD}$， $\mathit{BC}$， $\mathit{BD}$于点 $E$， $F$， $O$（尺规作图，不写作法，保留作图痕迹）；

（2）连接 $\mathit{BE}$， $\mathit{DF}$，求证：四边形 $\mathit{BEDF}$为菱形．

如图，在菱形 $\mathit{ABCD}$中， $E$， $F$是对角线 $\mathit{AC}$上的两点，且 $\mathit{AE}=\mathit{CF}$．

（1）求证： $\mathit{\Delta ABE}\cong \mathit{\Delta CDF}$；

（2）证明四边形 $\mathit{BEDF}$是菱形．

如图，在 $\text{Rt}\Delta \text{ABC}$中， $\angle \mathit{ACB}=90°$．线段 $\mathit{EF}$是由线段 $\mathit{AB}$平移得到的，点 $F$在边 $\mathit{BC}$上， $\mathit{\Delta EFD}$是以 $\mathit{EF}$为斜边的等腰直角三角形，且点 $D$恰好在 $\mathit{AC}$的延长线上．

（1）求证： $\angle \mathit{ADE}=\angle \mathit{DFC}$；

（2）求证： $\mathit{CD}=\mathit{BF}$．

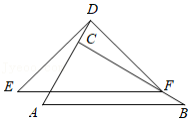
在《阿基米德全集》中的《引理集》中记录了古希腊数学家阿基米德提出的有关圆的一个引理．如图，已知 $\stackrel{̂}{\mathit{AB}}$， $C$是弦 $\mathit{AB}$上一点，请你根据以下步骤完成这个引理的作图过程．

（1）尺规作图（保留作图痕迹，不写作法）；

①作线段 $\mathit{AC}$的垂直平分线 $\mathit{DE}$，分别交 $\stackrel{̂}{\mathit{AB}}$于点 $D$， $\mathit{AC}$于点 $E$，连接 $\mathit{AD}$， $\mathit{CD}$；

②以点 $D$为圆心， $\mathit{DA}$长为半径作弧，交 $\stackrel{̂}{\mathit{AB}}$于点 $F(F$， $A$两点不重合），连接 $\mathit{DF}$， $\mathit{BD}$， $\mathit{BF}$．

（2）直接写出引理的结论：线段 $\mathit{BC}$， $\mathit{BF}$的数量关系．

如图，在 $\text{Rt}\Delta \text{ABC}$中， $\angle A=90°$，作 $\mathit{BC}$的垂直平分线交 $\mathit{AC}$于点 $D$，延长 $\mathit{AC}$至点 $E$，使 $\mathit{CE}=\mathit{AB}$．

（1）若 $\mathit{AE}=1$，求 $\mathit{\Delta ABD}$的周长；

（2）若 $\mathit{AD}=\frac{1}{3}\mathit{BD}$，求 $\tan \angle \mathit{ABC}$的值．

如图，已知 $\mathit{\Delta ABC}$中， $D$是 $\mathit{AC}$的中点，过点 $D$作 $\mathit{DE}\perp \mathit{AC}$交 $\mathit{BC}$于点 $E$，过点 $A$作 $\mathit{AF}//\mathit{BC}$交 $\mathit{DE}$于点 $F$，连接 $\mathit{AE}$、 $\mathit{CF}$．

（1）求证：四边形 $\mathit{AECF}$是菱形；

（2）若 $\mathit{CF}=2$， $\angle \mathit{FAC}=30°$， $\angle B=45°$，求 $\mathit{AB}$的长．

人教版初中数学教科书八年级上册第 $35-36$页告诉我们作一个三角形与已知三角形全等的方法：

已知： $\mathit{\Delta ABC}$． 求作：△ $A\text{'}B\text{'}C\text{'}$，使得△ $A\text{'}B\text{'}C\text{'}\cong \mathit{\Delta ABC}$． 作法：如图． （1）画 $B^{\text{'}}C\text{'}=\mathit{BC}$； （2）分别以点 $B\text{'}$， $C\text{'}$为圆心，线段 $\mathit{AB}$， $\mathit{AC}$长为半径画弧，两弧相交于点 $A\text{'}$； （3）连接线段 $A\text{'}B\text{'}$， $A\text{'}C\text{'}$，则△ $A\text{'}B\text{'}C\text{'}$即为所求作的三角形．

请你根据以上材料完成下列问题：

（1）完成下面证明过程（将正确答案填在相应的空上） $:$

证明：由作图可知，在△ $A\text{'}B\text{'}C\text{'}$和 $\mathit{\Delta ABC}$中，

$\left\{\begin{array}{c}B\text{'}C\text{'}=\mathit{BC}\\ A\text{'}B\text{'}=\left(\right)\\ A\text{'}C\text{'}=\left(\right)\end{array}\right.$

$\therefore$△ $A^{\text{'}}{B}^{\text{'}}C\text{'}\cong$　　．

（2）这种作一个三角形与已知三角形全等的方法的依据是 　　．（填序号）

① $\mathit{AAS}$

② $\mathit{ASA}$

③ $\mathit{SAS}$

④ $\mathit{SSS}$