如图,在矩形 中,点 在边 上,点 在 的延长线上,且 .
求证:(1) ;
(2)四边形 是平行四边形.

四边形 为矩形, 是 延长线上的一点.
(1)若 ,如图1,求证:四边形 为平行四边形;
(2)若 ,点 是 上的点, , 于点 ,如图2,求证: 是等腰直角三角形.

在 中, , 是中线, ,一个以点 为顶点的 角绕点 旋转,使角的两边分别与 、 的延长线相交,交点分别为点 、 , 与 交于点 , 与 交于点 .

(1)如图1,若 ,求证: ;
(2)如图2,在 绕点 旋转的过程中,试证明 恒成立;
(3)若 , ,求 的长.
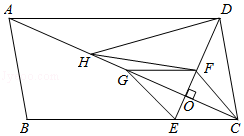
如图,在 中, 于点O,交BC于点E, , 交DE于点F,连接 ,点H为线段 上一点,连接 .
(1)判断四边形 的形状,并说明理由;
(2)当 时,求证: .
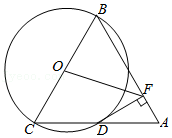
如图,在 中, , ,点C是 的中点,以OC为半径作 .
(1)求证: 是 的切线;
(2)若 ,求 的长.

《淮南子 天文训》中记载了一种确定东西方向的方法,大意是:日出时,在地面上点 处立一根杆,在地面上沿着杆的影子的方向取一点 ,使 , 两点间的距离为10步(步是古代的一种长度单位),在点 处立一根杆;日落时,在地面上沿着点 处的杆的影子的方向取一点 ,使 , 两点间的距离为10步,在点 处立一根杆.取 的中点 ,那么直线 表示的方向为东西方向.
(1)上述方法中,杆在地面上的影子所在直线及点 , , 的位置如图所示.使用直尺和圆规,在图中作 的中点 (保留作图痕迹);

(2)在如图中,确定了直线 表示的方向为东西方向.根据南北方向与东西方向互相垂直,可以判断直线 表示的方向为南北方向,完成如下证明.
证明:在 中, , 是 的中点,
(填推理的依据).
直线 表示的方向为东西方向,
直线 表示的方向为南北方向.
如图, 中, , ,点 ,点 ,反比例函数 的图象经过点 .
(1)求反比例函数的解析式;
(2)将直线 向上平移 个单位后经过反比例函数 图象上的点 ,求 , 的值.

如图,在等边三角形 中,点 是边 上一定点,点 是直线 上一动点,以 为一边作等边三角形 ,连接 .
【问题解决】
如图1,若点 在边 上,求证: ;
【类比探究】
如图2,若点 在边 的延长线上,请探究线段 , 与 之间存在怎样的数量关系?并说明理由.
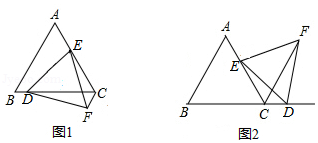
如图,在平行四边形 中, , 分别平分 和 ,交对角线 于点E,F.
(1)若 ,求 的度数;
(2)求证: .

如图, 是 的角平分线,在 上取点 ,使 .
(1)求证: ;
(2)若 , ,求 的度数.

如图,以等边三角形 的 边为直径画圆,交 于点 , 于点 ,连接 ,且 .
(1)求证: 是 的切线;
(2)求线段 的长度.