综合与实践
问题情境:数学活动课上,王老师出示了一个问题:
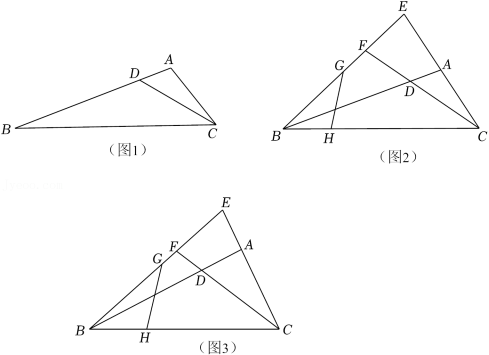
如图1,在
中,
是
上一点,
.求证
.
独立思考:(1)请解答王老师提出的问题.
实践探究:(2)在原有问题条件不变的情况下,王老师增加下面的条件,并提出新问题,请你解答.
“如图2,延长
至点
,使
,
与
的延长线相交于点
,点
分别在
上,
.在图中找出与
相等的线段,并证明.”
问题解决:(3)数学活动小组同学对上述问题进行特殊化研究之后发现,当
时,若给出
中任意两边长,则图3中所有已经用字母标记的线段长均可求.该小组提出下面的问题,请你解答.
“如图3,在(2)的条件下,若
,求
的长.”