我们定义:有一组邻角相等的凸四边形叫做“等邻角四边形”
(1)概念理解:
请你根据上述定义举一个等邻角四边形的例子;
(2)问题探究:
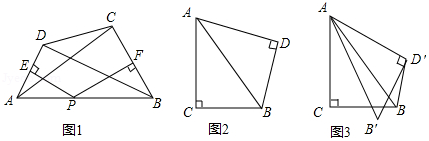
如图1,在等邻角四边形 中, , , 的中垂线恰好交于 边上一点 ,连接 , ,试探究 与 的数量关系,并说明理由;
(3)应用拓展:
如图2,在 与 中, , , ,将 绕着点 顺时针旋转角 得到 △ (如图 ,当凸四边形 为等邻角四边形时,求出它的面积.
推荐套卷
我们定义:有一组邻角相等的凸四边形叫做“等邻角四边形”
(1)概念理解:
请你根据上述定义举一个等邻角四边形的例子;
(2)问题探究:
如图1,在等邻角四边形 中, , , 的中垂线恰好交于 边上一点 ,连接 , ,试探究 与 的数量关系,并说明理由;
(3)应用拓展:
如图2,在 与 中, , , ,将 绕着点 顺时针旋转角 得到 △ (如图 ,当凸四边形 为等邻角四边形时,求出它的面积.
