已知在纸面上有一数轴(如图),折叠纸面.(1)若表示数1的点与表示数-1的点重合,则表示-2的点与表示数 的点重合;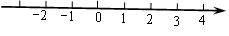
(2)若表示数-1的点与表示数3的点重合,回答以下问题:
① 表示数5的点与表示数 的点重合;
②若数轴上A、B两点之间的距离为9(A在B的左侧),且A、B两点经折叠后重合,求A、B两点表示的数是多少?
相关知识点
推荐套卷
已知在纸面上有一数轴(如图),折叠纸面.(1)若表示数1的点与表示数-1的点重合,则表示-2的点与表示数 的点重合;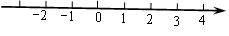
(2)若表示数-1的点与表示数3的点重合,回答以下问题:
① 表示数5的点与表示数 的点重合;
②若数轴上A、B两点之间的距离为9(A在B的左侧),且A、B两点经折叠后重合,求A、B两点表示的数是多少?