己知函数
(1)若 是
是 的极值点,求
的极值点,求 在
在 上的最大值;
上的最大值;
(2)在(1)的条件下,是否存在实数b,使得函数 的图象与函数
的图象与函数 的图象恰有3个交点,若存在,请求出实数b的取值范围;若不存在,试说明理由.
的图象恰有3个交点,若存在,请求出实数b的取值范围;若不存在,试说明理由.
已知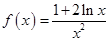 .
.
(1)求 的单调区间;
的单调区间;
(2)令 ,则
,则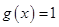 时有两个不同的根,求
时有两个不同的根,求 的取值范围;
的取值范围;
(3)存在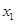 ,
,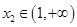 且
且 ,使
,使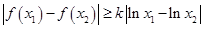 成立,求
成立,求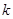 的取值范围.
的取值范围.
已知 ,函数
,函数 的零点从小到大依次为
的零点从小到大依次为 ,
, .
.
(Ⅰ)若 (
( ),试写出所有的
),试写出所有的 值;
值;
(Ⅱ)若 ,
, ,
, ,求证:
,求证:  ;
;
(Ⅲ)若 ,
, ,
, ,试把数列
,试把数列 的前
的前 项及
项及 按从小到大的顺序排列。(只要求写出结果).
按从小到大的顺序排列。(只要求写出结果).
【原创】(本小题满分12分)已知.
(Ⅰ)求函数的最小正周期和对称中心;
(Ⅱ)将函数的图象向右平移 个单位,得到函数
个单位,得到函数 的图象,当时,方程
的图象,当时,方程 有实数解,求实数的取值范围.
有实数解,求实数的取值范围.
(本小题满分14分)平面内一动点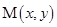 到定点
到定点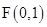 和到定直线
和到定直线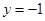 的距离相等,设
的距离相等,设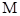 的轨迹是曲线
的轨迹是曲线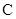 .
.
(1)求曲线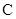 的方程;
的方程;
(2)在曲线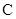 上找一点
上找一点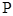 ,使得点
,使得点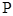 到直线
到直线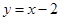 的距离最短,求出
的距离最短,求出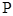 点的坐标;
点的坐标;
(3)设直线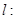
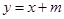 ,问当实数
,问当实数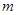 为何值时,直线
为何值时,直线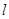 与曲线
与曲线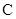 有交点?
有交点?
已知函数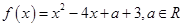
(1)若函数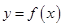 的图象与x轴无交点,求a的取值范围;
的图象与x轴无交点,求a的取值范围;
(2) 若函数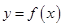 在[-1,1]上存在零点,求a的取值范围;
在[-1,1]上存在零点,求a的取值范围;
(3)设函数 ,当
,当 时,若对任意的
时,若对任意的 ,总存在
,总存在 ,使得
,使得 ,求b的取值范围.
,求b的取值范围.
(本小题满分12分)甲厂根据以往的生产销售经验得到下面有关生产销售的统计规律:每生产产品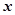 (百台),其总成本为
(百台),其总成本为 (万元),其中固定成本为
(万元),其中固定成本为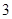 万元,并且每生产1百台的生产成本为1万元(总成本
万元,并且每生产1百台的生产成本为1万元(总成本 固定成本+生产成本),销售收入
固定成本+生产成本),销售收入 ,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题
,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题
(1)写出利润函数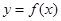 的解析式(利润
的解析式(利润 销售收入—总成本);
销售收入—总成本);
(2)甲厂生产多少台新产品时,可使盈利最多?
已知函数f(x)=
(Ⅰ)求f(1),f(﹣3),f(a+1)的值;
(Ⅱ)求函数f(x)的零点.