河南省信阳高中高三上学期第八次大考数学试卷
下列命题中,正确的是 ( ).
A.存在 ,使得 ,使得 |
B.“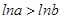 ”是“ ”是“ ”的充要条件 ”的充要条件 |
C.若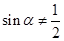 ,则 ,则 |
D.若函数 在 在 有极值 有极值 ,则 ,则 或 或 |
如图是一个无盖器皿的三视图,正视图、侧视图和俯视图中的正方形边长为2,正视图、侧视图中的虚线都是半圆,则该器皿的表面积是( )
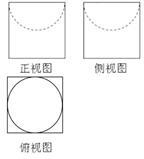
A. |
B.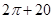 |
C. |
D.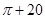 |
平行四边形 中,
中, ·
· =0,沿BD将四边形折起成直二面角A一BD-C,且
=0,沿BD将四边形折起成直二面角A一BD-C,且 ,则三棱锥
,则三棱锥 的外接球的表面积为( )
的外接球的表面积为( )
A. |
B. |
C. |
D. |
已知函数 是
是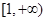 上的增函数.当实数
上的增函数.当实数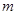 取最大值时,若存在点
取最大值时,若存在点 ,使得过点
,使得过点 的直线与曲线
的直线与曲线 围成两个封闭图形,且这两个封闭图形的面积总相等,则点
围成两个封闭图形,且这两个封闭图形的面积总相等,则点 的坐标为( )
的坐标为( )
A. |
B. |
C. |
D. |
已知中心在原点,焦点在坐标轴上的双曲线与圆 有公共点
有公共点 ,且圆在
,且圆在 点的切线与双曲线的渐近线平行,则双曲线的离心率为( )
点的切线与双曲线的渐近线平行,则双曲线的离心率为( )
A. |
B. |
C. 或 或 |
D.以上都不对 |
已知双曲线C的方程为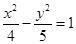 ,其左、右焦点分别是
,其左、右焦点分别是 、
、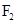 .已知点
.已知点 坐标为
坐标为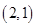 ,双曲线
,双曲线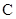 上点
上点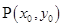 (
( ,
,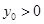 )满足
)满足 ,则
,则 ( )
( )
A.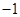 |
B. |
C.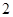 |
D.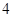 |
已知定义在 上的函数
上的函数 满足
满足 ,当
,当 时,
时, ,设
,设 在
在 上的最大值为
上的最大值为 ,且
,且 的前
的前 项和为
项和为 ,则
,则 =( ).
=( ).
A. |
B. |
C. |
D. |
设函数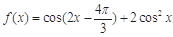 ,
,
(Ⅰ)求 的最大值,并写出使
的最大值,并写出使 取最大值时x的集合;
取最大值时x的集合;
(Ⅱ)已知 中,角A、B、C的对边分别为a、b、c,若
中,角A、B、C的对边分别为a、b、c,若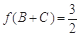 ,
, ,求
,求 的面积的最大值.
的面积的最大值.
已知数列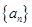 的前
的前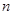 项和为
项和为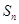 ,且
,且 .
.
(1)求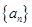 的通项公式;
的通项公式;
(2)设 ,若
,若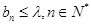 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(3)设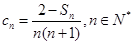 ,
, 是数列
是数列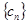 的前
的前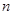 项和,证明
项和,证明 .
.
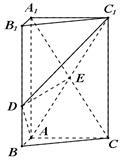
如图,三棱柱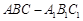 中,
中,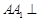 平面
平面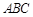 ,
,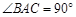 ,
,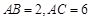 , 点
, 点 在线段
在线段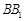 上,且
上,且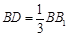 ,
, .
.
(Ⅰ)求证:直线 与平面
与平面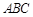 不平行;
不平行;
(Ⅱ)设平面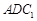 与平面
与平面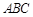 所成的锐二面角为
所成的锐二面角为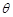 ,若
,若 ,求
,求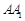 的长;
的长;
(Ⅲ)在(Ⅱ)的条件下,设平面 平面
平面 ,求直线
,求直线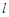 与
与 所成的角的余弦值.
所成的角的余弦值.
已知椭圆 的下顶点为P(0,-1),
的下顶点为P(0,-1), 到焦点的距离为
到焦点的距离为 .
.
(Ⅰ)设Q是椭圆上的动点,求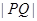 的最大值;
的最大值;
(Ⅱ)若直线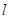 与圆O:x2+y2=1相切,并与椭圆
与圆O:x2+y2=1相切,并与椭圆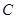 交于不同的两点A、B.当
交于不同的两点A、B.当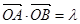 ,且满足
,且满足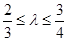 时,求
时,求 AOB面积S的取值范围.
AOB面积S的取值范围.
已知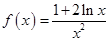 .
.
(1)求 的单调区间;
的单调区间;
(2)令 ,则
,则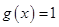 时有两个不同的根,求
时有两个不同的根,求 的取值范围;
的取值范围;
(3)存在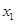 ,
,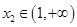 且
且 ,使
,使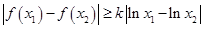 成立,求
成立,求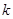 的取值范围.
的取值范围.
选修4-1:几何证明选讲
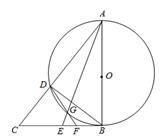
如图, 是
是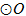 的直径,
的直径,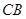 与
与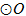 相切于
相切于 ,
,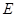 为线段
为线段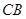 上一点,连接
上一点,连接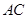 、
、 分别交
分别交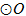 于
于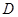 、
、 两点,连接
两点,连接 交
交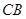 于点
于点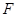 .
.
(Ⅰ)求证: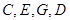 四点共圆;
四点共圆;
(Ⅱ)若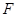 为
为 的三等分点且靠近
的三等分点且靠近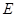 ,
,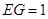 ,
, ,求线段
,求线段 的长.
的长.
选修4-4:坐标系与参数方程选讲
已知在直角坐标系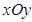 中,直线
中,直线 的参数方程为
的参数方程为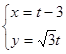 ,(
,(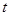 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,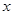 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线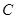 的极坐标方程为
的极坐标方程为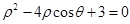 .
.
(Ⅰ)求直线 的普通方程和曲线
的普通方程和曲线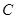 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设点 是曲线
是曲线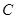 上的一个动点,求它到直线
上的一个动点,求它到直线 的距离
的距离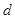 的取值范围.
的取值范围.
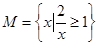 ,
,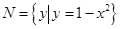 ,则
,则 ( ).
( ).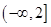
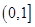

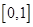
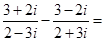 ( )
( )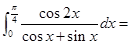 ( )
( )
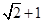
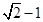
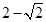
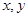 满足不等式组
满足不等式组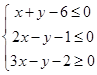 ,若
,若 的最大值为
的最大值为 ,最小值为
,最小值为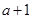 ,则实数
,则实数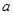 的取值范围为( )
的取值范围为( )

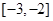

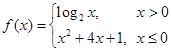 ,若实数
,若实数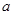 满足
满足 =1,则实数
=1,则实数

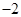
 在区间
在区间 上恒有
上恒有  ,则关于
,则关于 的不等式
的不等式 的解集为_______.
的解集为_______.
 ,当正数
,当正数 、
、 变化时,
变化时,  也在变化,则
也在变化,则 的最大值为 .
的最大值为 . 中,已知
中,已知 ,
, ,则
,则 的值是 .
的值是 .
 在
在 上是增函数,函数
上是增函数,函数 ,当
,当 时,函数
时,函数 的最大值
的最大值 与最小值
与最小值 的差为
的差为 ,则
,则 .
.
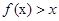 的解集;
的解集;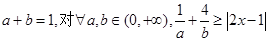 -
-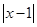 恒成立,求
恒成立,求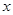 的取值范围.
的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号