【原创】(本小题满分12分)已知.
(Ⅰ)求函数的最小正周期和对称中心;
(Ⅱ)将函数的图象向右平移 个单位,得到函数
个单位,得到函数 的图象,当时,方程
的图象,当时,方程 有实数解,求实数的取值范围.
有实数解,求实数的取值范围.
已知 .
.
(1)求 的单调区间;
的单调区间;
(2)令 ,则
,则 时有两个不同的根,求
时有两个不同的根,求 的取值范围;
的取值范围;
(3)存在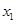 ,
,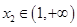 且
且 ,使
,使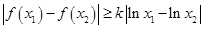 成立,求
成立,求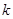 的取值范围.
的取值范围.
(本小题满分13分)已知函数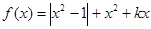 .
.
(1)若对于区间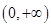 内的任意
内的任意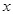 ,总有
,总有 成立,求实数
成立,求实数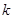 的取值范围;
的取值范围;
(2)若函数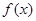 在区间
在区间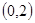 内有两个不同的零点
内有两个不同的零点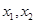 ,求:
,求:
①实数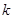 的取值范围; ②
的取值范围; ②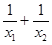 的取值范围.
的取值范围.
(本题满分14分)设 为函数
为函数 两个不同零点.
两个不同零点.
(Ⅰ)若 ,且对任意
,且对任意 ,都有
,都有 ,求
,求 ;
;
(Ⅱ)若 ,则关于
,则关于 的方程
的方程 是否存在负实根?若存在,求出该负根的取值范围,若不存在,请说明理由;
是否存在负实根?若存在,求出该负根的取值范围,若不存在,请说明理由;
(Ⅲ)若 ,
, ,且当
,且当 时,
时, 的最大值为
的最大值为 ,求
,求 的最小值.
的最小值.
(本小题满分10分)对于给定的函数 ,定义
,定义 如下:
如下: ,其中
,其中 .
.
(1)当 时,求证:
时,求证: ;
;
(2)当 时,比较
时,比较 与
与 的大小;
的大小;
(3)当 时,求
时,求 的不为0的零点.
的不为0的零点.
(本小题满分16分)已知函数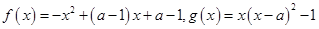 ,其中a为实数.
,其中a为实数.
(1)是否存在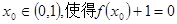 ?若存在,求出实数a的取值范围;若不存在,请说明理由.
?若存在,求出实数a的取值范围;若不存在,请说明理由.
(2)若集合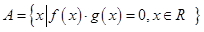 中恰有5个元素,求实数a的取值范围.
中恰有5个元素,求实数a的取值范围.
已知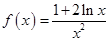 .
.
(1)求 的单调区间;
的单调区间;
(2)令 ,则
,则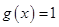 时有两个不同的根,求
时有两个不同的根,求 的取值范围;
的取值范围;
(3)存在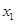 ,
,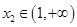 且
且 ,使
,使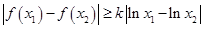 成立,求
成立,求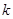 的取值范围.
的取值范围.
设函数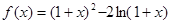
(1)若关于 的不等式
的不等式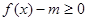 在
在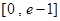 有实数解,求实数
有实数解,求实数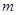 的取值范围;
的取值范围;
(2)设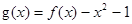 ,若关于
,若关于 的方程
的方程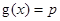 至少有一个解,求
至少有一个解,求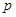 的最小值.
的最小值.
(3)证明不等式: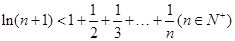
已知 ,函数
,函数 的零点从小到大依次为
的零点从小到大依次为 ,
, .
.
(Ⅰ)若 (
( ),试写出所有的
),试写出所有的 值;
值;
(Ⅱ)若 ,
, ,
, ,求证:
,求证:  ;
;
(Ⅲ)若 ,
, ,
, ,试把数列
,试把数列 的前
的前 项及
项及 按从小到大的顺序排列。(只要求写出结果).
按从小到大的顺序排列。(只要求写出结果).
(本题满分18分)本题共3小题,第(1)小题6分,第(2)小题6分,第(3)小题6分.
已知函数 .
. 
(1)指出 的基本性质(结论不要求证明)并作出函数
的基本性质(结论不要求证明)并作出函数 的图像;
的图像;
(2)关于 的不等式
的不等式 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(3)关于 的方程
的方程 (
( )恰有6个不同的实数解,求
)恰有6个不同的实数解,求 的取值范围.
的取值范围.
(本小题满分14分)平面内一动点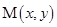 到定点
到定点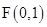 和到定直线
和到定直线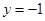 的距离相等,设
的距离相等,设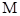 的轨迹是曲线
的轨迹是曲线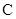 .
.
(1)求曲线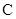 的方程;
的方程;
(2)在曲线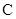 上找一点
上找一点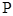 ,使得点
,使得点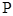 到直线
到直线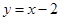 的距离最短,求出
的距离最短,求出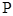 点的坐标;
点的坐标;
(3)设直线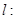
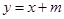 ,问当实数
,问当实数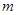 为何值时,直线
为何值时,直线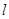 与曲线
与曲线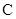 有交点?
有交点?