重庆小面是重庆美食的名片之一,深受外地游客和本地民众欢迎.某面馆向食客推出经典特色重庆小面,顾客可到店食用(简称“堂食”小面),也可购买搭配佐料的袋装生面(简称“生食”小面).已知 份“堂食”小面和 份“生食”小面的总售价为 元, 份“堂食”小面和 份“生食”小面的总售价为 元.
(1)求每份“堂食”小面和“生食”小面的价格分别是多少元?
(2)该面馆在4月共卖出“堂食”小面 份,“生食”小面 份.为回馈广大食客,该面馆从5月1日起每份“堂食”小面的价格保持不变,每份“生食”小面的价格降低 .统计5月的销量和销售额发现:“堂食”小面的销量与4月相同,“生食”小面的销量在4月的基础上增加了 ,这两种小面的总销售额在4月的基础上增加了 .求 的值.
已知关于 的方程 有两个正整数根( 是整数). 的三边 、 满足 .
求:(1) 的值;
(2) 的面积.
定义:如果一元二次方程 满足 ,那么我们称这个方程为“凤凰方程”,已知 是“凤凰方程”,且有两个相等的实数根,求 之间的关系.
已知关于 的一元二次方程 .
(1)求证:无论 取何值,方程都有两个不相等的实数根.
(2)如果方程的两个实数根为 ,且 与 都为整数,求 所有可能的值.
设 是不小于 的实数,关于 的方程 有两个不相等的实数根 .
(1)若 ,求 的值;
(2)求 的最大值.
在平面直角坐标系 中,抛物线 过点 .
(1)求抛物线的解析式;
(2)平移抛物线,平移后的顶点为 .
ⅰ.如果 ,设直线 ,在这条直线的右侧原抛物线和新抛物线均呈上升趋势,求k的取值范围;
ⅱ.点 在原抛物线上,新抛物线交 轴于点 ,且 ,求点 的坐标.
如图所示,在等腰三角形 中, ,点 在线段 上,点 在线段 上,且 .
求证:(1) ;
(2) .
我们经常会采用不同方法对某物体进行测量,请测量下列灯杆 的长.
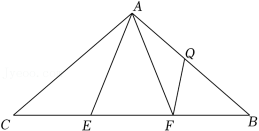
(1)如图(1)所示,将一个测角仪放置在距离灯杆 底部 米的点 处,测角仪高为 米,从 点测得 点的仰角为 ,求灯杆 的高度.(用含 的代数式表示)
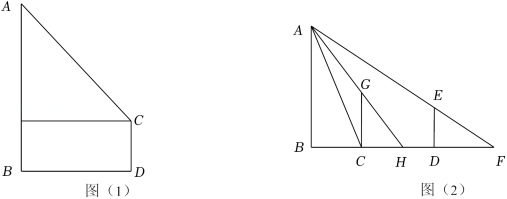
(2)我国古代数学家赵爽利用影子对物体进行测量的方法,在至今仍有借鉴意义.如图(2)所示,现将一高度为 米的木杆 放在灯杆 前,测得其影长 为 米,再将木杆沿着 方向移动 米至 的位置,此时测得其影长 为 米,求灯杆 的高度.
一个一次函数的截距为 ,且经过点 .
(1)求这个一次函数的解析式;
(2)点 在某个反比例函数上,点 横坐标为 ,将点 向上平移 个单位得到点 ,求 的值.