2021年,黄冈、咸宁、孝感三市实行中考联合命题,为确保联合命题的公平性,决定采取三轮抽签的方式来确定各市选派命题组长的学科.第一轮,各市从语文、数学、英语三个学科中随机抽取一科;第二轮,各市从物理、化学、历史三个学科中随机抽取一科;第三轮,各市从道德与法治、地理、生物三个学科中随机抽取一科.
(1)黄冈在第一轮抽到语文学科的概率是_____.
(2)用画树状图或列表法求黄冈在第二轮和第三轮抽签中,抽到的学科恰好是历史和地理的概率.
如图,已知矩形 与 三边都相切,与 交于点 .已知点 分别从 三点同时出发,沿矩形 的边逆时针方向匀速运动,点 的运动速度分别是 ,当点 到达点 时停止运动, 两点同时停止运动.设运动时间为 (单位: ).
(1)求证: ;
(2)设 ,当 与 相似时,求出 的值;
(3)设 关于直线 对称的图形是 ,当 和 分别为何值时,点 与圆心 恰好重合,求出符合条件的 的值.

如图,已知抛物线 与 轴相交于 两点,与 轴的正半轴相交于 点,过 三点的 与 轴相切于点 .
(1)请求出点 坐标和 的半径;
(2)请确定抛物线的解析式;
(3) 为 轴负半轴上的一个动点,直线 交 于点 .若 与以 为顶点的三角形相似,求 的值(先画出符合题意的示意图再求解).

如图,锐角 中, 的对边分别是 ,已知二次函数 的图象顶点与点 关于 轴对称.延长 至 点,使 ,且以 为圆心, 为半径的圆与以 为圆心 为半径的圆相外切.
(1)求 的度数;
(2)设 ,求 的值;
(3)若关于 的方程 的两个根 满足 ,求 的面积.

如图,已知直线 ,与 轴交于点 ,与 轴交于点 ,以 为直径的 交 于另一点 ,把弧 沿直线 翻转后与 交于点 .
(1)当 时,求 的长;
(2)是否存在实数 ,使沿直线 把弧 翻转后所得的弧与 相切?若存在,请求出此时 的值;若不存在,请说明理由.

如图所示,在平面直角坐标系中, 与 轴交于 (且 两点,与 轴相切于点 .
(1)求点 的坐标和 的值;
(2)求过点 的抛物线解析式;
(3)若抛物线顶点为 ,判断点 与 的位置关系,并求出 的外接圆半径.

如图①, 为第一象限内一点,过 两点的 交 轴正半轴于点 ,交 轴正半轴于点 .
(1)求证: 平分 ;
(2)作 交弦 于点 .
①若 ,求 的长;
②若 ,把 沿 轴翻折,得到 (如图②),求 的长.

如图, 是半圆的直径,弦 ,过点 的切线交 的延长线于点 交 的延长线于点 .求证: .
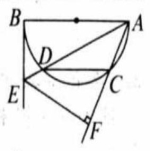
如图, 是 的直径, 是弧 的中点,延长 至 ,使 ,连接 是 的中点, 的延长线交 的延长线于点 交 于点 ,连接 .
(1)求证: 是 的切线;
(2)若 ,求 的长.
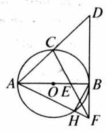
如图所示, 中, ,过点 作 的外接圆的切线交 的延长线于点 ,过点 作 交 的延长线于点 ,求证: .
等腰直角 和 如图放置,已知 的半径为 ,圆心 与直线 的距离为5,现 以每秒2个单位的速度向右移动,同时 的边长 又以每秒 个单位沿 方向增大.
(1)当 的边( 边除外)与圆第一次相切时,点 移动了多少距离?
(2)若 在移动的同时, 也以每秒 个单位的速度向右移动,则 从开始移动,到它的边与圆最后一次相切,一共经过了多少时间?
(3)在(2)条件下,是否存在某一时刻, 与 的公共部分等于 的面积?若存在,求出恰好符合条件时两个图形移动了多少时间?若不存在,请说明理由.

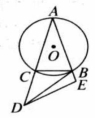
如图, 是 上两点,且 ,连接 并延长到点 ,使 ,连接 .
(1)求证: 是 的切线;
(2)点 分别是 的中点, 所在直线交 于点 ,求 的长.
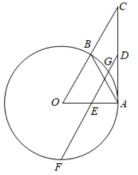
如图, 为 的直径,点 为 上异于 的一动点,弦 , 是关于 的一元二次方程 的两根,求 的最大值.
