初中数学解答题

如图，已知在 $△\mathit{ABC}$中， $\mathit{AB}>\mathit{AC},\angle \mathit{BAC}={45}^{\circ },E$是 $\angle \mathit{BAC}$的外角平分线与 $△\mathit{ABC}$的外接圆的交点，点 $F$在 $\mathit{AB}$上且 $\mathit{EF}\perp \mathit{AB}$，已知 $\mathit{AF}=1,\mathit{BF}=5$，求 $△\mathit{ABC}$的面积.

如图，已知在 $△\mathit{ABC}$中， $\mathit{AB}>\mathit{AC},\angle A$的外角平分线交 $△\mathit{ABC}$的外接圆于点 $E$，过 $E$作 $\mathit{EF}\perp \mathit{AB}$，垂足为 $F$，求证: $\mathit{AB}-\mathit{AC}=2\mathit{AF}$.

如图，点 $I$是 $△\mathit{ABC}$的内心， $\mathit{AB}\ne \mathit{AC}$，过点 $I$作一圆与边 $\mathit{AB}$相切于点 $B$，与直线 $\mathit{AC}$交于点 $D$和点 $E$，连接 $\mathit{BE}$，若 $\angle \mathit{ABC}={80}^{\circ },\angle \mathit{EBC}={30}^{\circ },\stackrel{⏜}{\mathit{BI}}=2\stackrel{⏜}{\mathit{DI}}$，求 $\angle \mathit{DIC}$的大小.

已知 $△\mathit{ABC}$内接于 $\odot O,\mathit{AB}=\mathit{AC},\angle \mathit{BAC}={42}^{\circ }$，点 $D$是 $\odot O$上一点.

（1）如图①，若 $\mathit{BD}$为 $\odot O$的直径，连接 $\mathit{CD}$，求 $\angle \mathit{DBC}$和 $\angle \mathit{ACD}$的大小；

（2）如图②，若 $\mathit{CD}//\mathit{BA}$，连接 $\mathit{AD}$，过点 $D$作 $\odot O$的切线，与 $\mathit{OC}$的延长线交于点 $E$，求 $\angle E$的大小.

如图所示，在 $\mathit{ABC}$中， $\mathit{AC}=\mathit{BC},\angle \mathit{ACB}={90}^{\circ },D,E$是边 $\mathit{AB}$上的两点， $\mathit{AD}=3,\mathit{BE}=4,\angle \mathit{DCE}={45}^{\circ }$.则 $△\mathit{ABC}$的面积是多少?

已知在 $△\mathit{ABC}$ 中， $\angle \mathit{ABC}={90}^{\circ }\mathrm{，}\mathit{AB}=\mathit{BC}$， 四边形 $\mathit{CDEF}$ 是正方形，连接 $\mathit{AE},G$是 $\mathit{AE}$的中点.

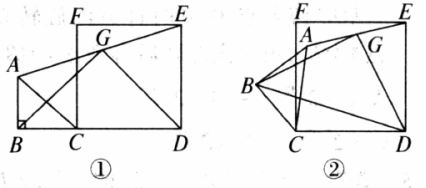
（1）如图①，当 $B,C,D$在一条直线上时，试判断 $\mathit{BG}$与 $\mathit{GD}$的位置关系，并求 $\frac{\mathit{BG}}{\mathit{GD}}$的值；

（2）如图②，当 $△\mathit{ABC}$绕点 $C$旋转后，（1）中结论是否仍然成立?试说明理由.

如图，在等腰直角三角形 $\mathit{ABC}$中， $\angle \mathit{ACB}={90}^{\circ },\mathit{AC}=\mathit{BC}=2\sqrt{5}$，边长为2的正方形 $\mathit{DEFC}$的对角线交点与点 $C$重合，连接 $\mathit{AD},\mathit{BE}$.

（1）求证: $△\mathit{ACD}\cong △\mathit{BCE}$；

（2）当点 $D$在 $△\mathit{ABC}$内部，且 $\angle \mathit{ADC}={90}^{\circ }$吋，设 $\mathit{AC}$与 $\mathit{DG}$相交于点 $M$，求 $\mathit{AM}$的长；

（3）将正方形 $\mathit{DEFG}$绕点 $C$旋转一周，当点 $A,D,E$三点在同一直线上时，请直接写出 $\mathit{AD}$的长.

如图， $P$为等边三角形 $\mathit{ABC}$内一点， $\mathit{PA}=3,\mathit{PB}=4,\mathit{PC}=5$，求 $△\mathit{ABC}$的面积.

如图，在正方形 $\mathit{ABCD}$中， $E,F$分别是边 $\mathit{BC},\mathit{CD}$上的点， $\angle \mathit{EAF}={45}^{\circ },△\mathit{ECF}$的周长为 $8$，求正方形 $\mathit{ABCD}$的面积.

如图， 在正方形 $\mathit{ABCD}$ 中， $\mathit{AB}=4$， 点 $M$ 在 $\mathit{CD}$ 边上， 且 $DM=1\mathrm{}$， $△AEM$与 $△\mathit{ADM}$关于 $\mathit{AM}$所在直线对称，将 $△\mathit{ADM}$按顺时针方向绕点 $A$旋转 ${90}^{\circ }$得到 $△\mathit{ABF}$，连接 $\mathit{EF}$，求线段 $\mathit{EF}$的长.

如图， 已知直线 $y=-\frac{1}{2}x$ 与拋物线 $y=-\frac{1}{4}{x}^2+6$ 交于 $A\mathrm{，}B$两点.

（1）求 $A,B$两点的坐标；

（2）求线段 $\mathit{AB}$的垂直平分线的解析式；

（3）取与线段AB等长的一根橡皮筋，端点分别固定在A，B两处，用铅笔拉着这根橡皮筋使笔尖 $P$在直线 $\mathit{AB}$上方的抛物线上移动，动点 $P$将与 $A,B$构成无数个三角形，这些三角形中是否存在一个面积最大的三角形?如果存在，求出最大面积，并指出此时点 $P$的坐标；如果不存在，请简要说明理由.

已知二次函数 $y=a{x}^2+\mathit{bx}+c$的图象开口向上，且经过点 $A\left(0,\frac{3}{2}\right),B\left(2,-\frac{1}{2}\right)$.

（1）求 $b$的值（用含 $a$的代数式表示）；

（2）若二次函数 $y=a{x}^2+\mathit{bx}+c$在 $1⩽x⩽3$时， $y$的最大值为1，求 $a$的值；

（3）将线段 $\mathit{AB}$向右平移 $2$个单位得到线段 $A^{\text{'}}{B}^{\text{'}}$.若线段 $A^{\text{'}}{B}^{\text{'}}$与抛物线 $y=a{x}^2+\mathit{bx}+c+4a-1$仅有一个交点，求 $a$的取值范围.

如图，抛物线 $y=a{x}^2+\mathit{bx}+c\left(a\ne 0\right)$与 $x$轴交于 $A,B$两点，与 $y$轴交于 $C$点， $\mathit{AC}=\sqrt{10},\mathit{OB}=\mathit{OC}=3\mathit{OA}$.

（1）求拋物线的解析式；

（2）在第二象限内的拋物线上确定一点 $P$，使四边形 $\mathit{PBAC}$的面积最大，求出点 $P$的坐标；

（3）在（2）的结论下，点 $M$为 $x$轴上一动点，抛物线上是否存在一点 $Q$，使点 $P,B,M,Q$为顶点的四边形是平行四边形，若存在，请直接写出 $Q$点的坐标；若不存在，请说明理由.

在某服装批发市场，某种品牌的时装当季节将来临时，价格呈上升趋势，设这种时装开始时定价为 $20$元，并且每周（ $7$天）涨价 $2$元，从第 $6$周开始保持 $30$元的价格平稳销售；从第 $12$周开始，当季节即将过去时，平均每周减价 $2$元，直到第 $16$周周末，该服装不再销售.

（1）试建立销售价 $y$与周次 $x$之间的函数关系式；

（2）若这种时装每件进价 $Z$与周次 $x$之间的关系为 $Z=-0.125{(x-8)}^2+12,1⩽x⩽16$，且 $x$为整数，试问该服装第几周出售时，每件销售利润最大，最大利润为多少?

已知二次函数 $y=x^2+bx-c$的图象经过两点 $P（1，a），Q（2，10a）$.

（1）如果 $a,b,c$都是整数，且 $c<b<8a$，求 $a,b,c$的值；

（2）设二次函数 $y=x^2+\mathit{bx}-c$的图象与 $x$轴的交点为 $A,B$，与 $y$轴的交点为 $C$.如果关于 $x$的方程 $x^2+\mathit{bx}-c=0$的两个根都是整数，求 $△\mathit{ABC}$的面积.