为了加强学生的体育锻炼,某班计划购买部分绳子和实心球.已知每条绳子的价格比每个实心球的价格少 元,且 元购买绳子的数量与 元购买实心球的数量相同.
(1)绳子和实心球的单价各是多少元?
(2)如果本次购买的总费用为 元,且购买绳子的数量是实心球数量的3倍,那么购买绳子和实心球的数量各是多少?
在贯彻落实“五育并举”的工作中,某校开设了五个社团活动:传统国学(A)、科技兴趣(B)、民族体育(C)、艺术鉴赏(D)、劳技实践(E),每个学生每个学期只参加一个社团活动.为了了解本学期学生参加社团活动的情况,学校随机抽取了若干名学生进行调查,并将调查结果绘制成如下两幅尚不完整的统计图.请根据统计图提供的信息,解答下列问题:
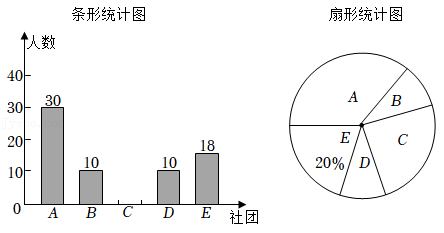
(1)本次调查的学生共有 人;
(2)将条形统计图补充完整;
(3)在扇形统计图中,传统国学(A)对应扇形的圆心角度数是 ;
(4)若该校有 名学生,请估算本学期参加艺术鉴赏(D)活动的学生人数.
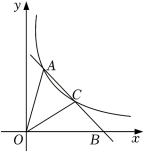
如图,直线 与反比例函数 的图象相交于点 和点 ,与 轴的正半轴相交于点 .
(1)求 的值;
(2)连接 ,若点 为线段 的中点,求 的面积.
新定义:我们把抛物线 (其中 )与抛物线 称为“关联抛物线”.例如:抛物线 的“关联抛物线”为: .已知抛物线 的“关联抛物线”为 .
(1)写出 的解析式(用含 的式子表示)及顶点坐标;
(2)若 ,过 轴上一点 ,作 轴的垂线分别交抛物线 , 于点 .
①当 时,求点 的坐标;
②当 时, 的最大值与最小值的差为 ,求 的值.
遵义市开展信息技术与教学深度融合的“精准化教学”,某实验学校计划购买A,B两种型号教学设备,已知A型设备价格比B型设备价格每台高 ,用 元购买A型设备的数量比用 元购买B型设备的数量多 台.
(1)求A,B型设备单价分别是多少元;
(2)该校计划购买两种设备共 台,要求A型设备数量不少于B型设备数量的 .设购买a台A型设备,购买总费用为 元,求 与 的函数关系式,并求出最少购买费用.
如图1所示是一种太阳能路灯,它由灯杆和灯管支架两部分构成.如图2, 是灯杆, 是灯管支架,灯管支架 与灯杆间的夹角 .综合实践小组的同学想知道灯管支架 的长度,他们在地面的点 处测得灯管支架底部 的仰角为 ,在点 处测得灯管支架顶部 的仰角为 ,测得 ( 在同一条直线上).根据以上数据,解答下列问题:
(1)求灯管支架底部距地面高度 的长(结果保留根号);
(2)求灯管支架 的长度(结果精确到 ,参考数据: ).

将正方形 和菱形 按照如图所示摆放,顶点 与顶点 重合,菱形 的对角线 经过点 ,点 分别在 上.
(1)求证: ;
(2)若 ,求 的长.

如图所示,甲、乙两个带指针的转盘分别被分成三个面积相等的扇形(两个转盘除表面数字不同外,其它完全相同),转盘甲上的数字分别是 ,转盘乙上的数字分别是 (规定:指针恰好停留在分界线上,则重新转一次).
(1)转动转盘,转盘甲指针指向正数的概率是_____;转盘乙指针指向正数的概率是_____.
(2)若同时转动两个转盘,转盘甲指针所指的数字记为 ,转盘乙指针所指的数字记为 ,请用列表法或树状图法求满足 的概率.

已知A、B两地之间有一条长440千米的高速公路.甲、乙两车分别从A、B两地同时出发,沿此公路相向而行,甲车先以100千米/时的速度匀速行驶200千米后与乙车相遇,再以另一速度继续匀速行驶4小时到达B地;乙车匀速行驶至A地,两车到达各自的目的地后停止,两车距A地的路程y(千米)与各自的行驶时间x(时)之间的函数关系如图所示.
(1)m= ,n= ;
(2)求两车相遇后,甲车距A地的路程y与x之间的函数关系式;
(3)当乙车到达A地时,求甲车距A地的路程.

党的十八大以来,我国把科技自立自强作为国家发展的战略支撑,科技事业发生了历史性、整体性、格局性变化,成功跨入创新型国家的行列,专利项目多项指数显著攀升.如图是长春市2016年到2020年专利授权情况的统计图.

根据以上信息回答下列问题:
(1)长春市从2016年到2020年,专利授权量最多的是 年;
(2)长春市从2016年到2020年,专利授权量年增长率的中位数是 ;
(3)与2019年相比,2020年长春市专利授权量增加了 件,专利授权量年增长率提高了 个百分点;(注:1%为1个百分点)
(4)根据统计图提供的信息,有下列说法,正确的画“√”,错误的画“×”.
①因为2019年的专利授权量年增长率最低,所以2019年的专利授权量的增长量就最小.
②与2018年相比,2019年的专利授权量年增长率虽然下降,但专利授权量仍然上升.这是因为专利授权量年增长率 ,所以只要专利授权量年增长率大于零,当年专利授权量就一定增加.
③通过统计数据,可以看出长春市区域科技创新力呈上升趋势,为国家科技自立自强贡献吉林力量.
如图,在Rt△ABC中, , .点D是AC的中点,过点D作DE⊥AC交BC于点E.延长ED至点F,使得DF=DE,连结AE、AF、CF.
(1)求证:四边形AECF是菱形;
(2)若 ,则 的值为 .

图①、图②、图③均是5×5的正方形网格,每个小正方形的边长均为1,其顶点称为格点,△ABC的顶点均在格点上.只用无刻度的直尺,在给定的网格中,按下列要求作图,保留作图痕迹.
(1)网格中△ABC的形状是 ;
(2)在图①中确定一点D,连结DB、DC,使△DBC与△ABC全等;
(3)在图②中△ABC的边BC上确定一点E,连结AE,使△ABE∽△CBA;
(4)在图③中△ABC的边AB上确定一点P,在边BC上确定一点Q,连结PQ,使△PBQ∽△ABC,且相似比为1:2.
