在平面直角坐标系中,点 是坐标原点,抛物线 经过点 ,对称轴为直线 .
(1)求 的值;
(2)已知点 在抛物线上,点 的横坐标为 ,点 的横坐标为 .过点 作 轴的垂线交直线 于点 ,过点 作 轴的垂线交直线 于点 .
(i)当 时,求 与 的面积之和;
(ii)在抛物线对称轴右侧,是否存在点 ,使得以 为顶点的四边形的面积为 ?若存在,请求出点 的横坐标 的值;若不存在,请说明理由.
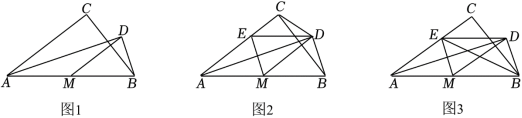
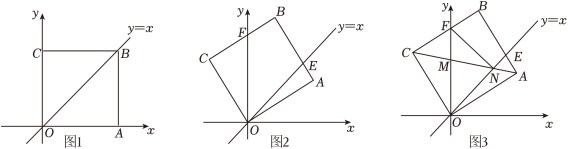
在 中, 是斜边 的中点,将线段 绕点 旋转至 位置,点 在直线 外,连接 .
(1)如图1,求 的大小;
(2)已知点 和边 上的点 满足 .
(i)如图2,连接 ,求证: ;
(ii)如图3,连接 ,若 ,求 的值.
端午节是中国的传统节日,民间有端午节吃粽子的习俗.在端午节来临之际,某校七、八年级开展了一次“包粽子”实践活动,对学生的活动情况按 分制进行评分,成绩(单位:分)均为不低于 的整数.为了解这次活动的效果,现从这两个年级各随机抽取 名学生的活动成绩作为样本进行整理,并绘制统计图表,部分信息如下:
八年级 名学生活动成绩统计表
|
成绩/分 |
6 |
7 |
8 |
9 |
10 |
|
人数 |
1 |
2 |
a |
b |
2 |
已知八年级 名学生活动成绩的中位数为 分.
请根据以上信息,完成下列问题:
(1)样本中,七年级活动成绩为 分的学生数是_____,七年级活动成绩的众数为 _____分;
(2) _____, _____;
(3)若认定活动成绩不低于 分为“优秀”,根据样本数据,判断本次活动中优秀率高的年级是否平均成绩也高,并说明理由.

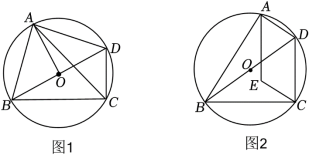
已知四边形 内接于 ,对角线 是 的直径.
(1)如图1,连接 ,若 ,求证: 平分 ;
(2)如图2, 为 内一点,满足 .若 , ,求弦 的长.
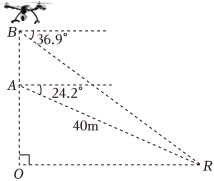
如图, 是同一水平线上的两点,无人机从 点竖直上升到 点时,测得 到 点的距离为 , 点的俯角为 ,无人机继续竖直上升到 点,测得 点的俯角为 .求无人机从 点到 点的上升高度 (精确到 ).
参考数据: .
【观察思考】
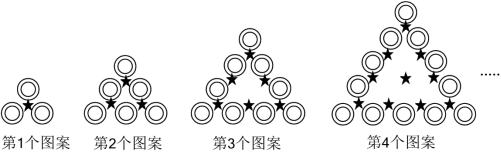
【规律发现】
请用含 的式子填空:
(1)第 个图案中“◎”的个数为_____;
(2)第1个图案中“★”的个数可表示为 ,第 个图案中“★”的个数可表示为 ,第 个图案中“★”的个数可表示为 ,第 个图案中“★”的个数可表示为 ,……,第 个图案中“★”的个数可表示为_____.
【规律应用】
(3)结合图案中“★”的排列方式及上述规律,求正整数 ,使得连续的正整数之和 等于第 个图案中“◎”的个数的 倍.
根据经营情况,公司对某商品在甲、乙两地的销售单价进行了如下调整:甲地上涨 ,乙地降价 元.已知销售单价调整前甲地比乙地少 元,调整后甲地比乙地少 元,求调整前甲、乙两地该商品的销售单价.
综合运用
如图1,在平面直角坐标系中,正方形 的顶点 在 轴的正半轴上.如图2,将正方形 绕点 逆时针旋转,旋转角为 , 交直线 于点 , 交 轴于点 .
(1)当旋转角 为多少度时, ;(直接写出结果,不要求写解答过程)
(2)若点 ,求 的长;
(3)如图3,对角线 交 轴于点 ,交直线 于点 ,连接 .将 与 的面积分别记为 与 .设 , ,求 关于 的函数表达式.
综合探究
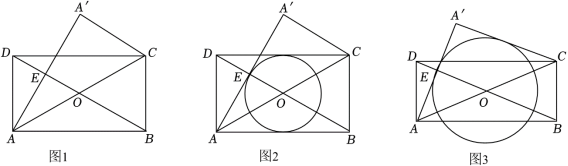
如图1,在矩形 中( ),对角线 相交于点 ,点 关于 的对称点为 .连接 交 于点 ,连接 .
(1)求证: ;
(2)以点 为圆心, 为半径作圆.
①如图2, 与 相切,求证: ;
②如图3, 与 相切, ,求 的面积.
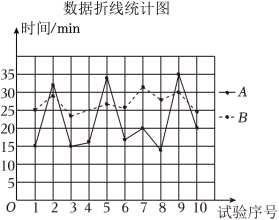
小红家到学校有两条公共汽车线路.为了解两条线路的乘车所用时间,小红做了试验,第一周( 个工作日)选择A线路,第二周( 个工作日)选择 线路,每天在固定时间段内乘车 次并分别记录所用时间.数据统计如下:(单位: )
数据统计表
|
实验序号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
A线路所用时间 |
15 |
32 |
15 |
16 |
34 |
18 |
21 |
14 |
35 |
20 |
|
B线路所用时间 |
25 |
29 |
23 |
25 |
27 |
26 |
31 |
28 |
30 |
24 |
根据以上信息解答下列问题:
|
平均数 |
中位数 |
众数 |
方差 |
|
|
A线路所用时间 |
22 |
a |
15 |
63.2 |
|
B线路所用时间 |
b |
26.5 |
c |
6.36 |
(1)填空:a=_____;b=_____;c=_____;
(2)应用你所学的统计知识,帮助小红分析如何选择乘车线路.
综合与实践
主题:制作无盖正方体形纸盒.
素材:一张正方形纸板.
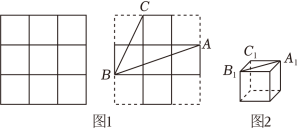
步骤1:如图1,将正方形纸板的边长三等分,画出九个相同的小正方形,并剪去四个角上的小正方形;
步骤2:如图2,把剪好的纸板折成无盖正方体形纸盒.
猜想与证明:(1)直接写出纸板上 与纸盒上 的大小关系;
(2)证明(1)中你发现的结论.
如图,在 中, .
(1)实践与操作:用尺规作图法过点 作 边上的高 ;(保留作图痕迹,不要求写作法)
(2)应用与计算:在(1)的条件下, ,求 的长.
2023年5月30日,神舟十六号载人飞船发射取得圆满成功,3名航天员顺利进驻中国空间站.如图中的照片展示了中国空间站上机械臂的一种工作状态.当两臂 ,两臂夹角 时,求 两点间的距离.(结果精确到 ,参考数据: )
