在习近平总书记视察广西、亲临柳州视察指导一周年之际,某校开展“紧跟伟大复兴领航人踔厉笃行”主题演讲比赛,演讲的题目有:《同甘共苦民族情》《民族团结一家亲,一起向未来》《画出最美同心圆》.赛前采用抽签的方式确定各班演讲题目,将演讲题目制成编号为 的 张卡片(如图所示,卡片除编号和内容外,其余完全相同).现将这 张卡片背面朝上,洗匀放好.
(1)某班从 张卡片中随机抽取 张,抽到卡片 的概率为_____;
(2)若七(1)班从 张卡片中随机抽取 张,记下题目后放回洗匀,再由七(2)班从中随机抽取 张,请用列表或画树状图的方法,求这两个班抽到不同卡片的概率.(这 张卡片分别用它们的编号 表示)

习近平总书记在主持召开中央农村工作会议中指出:“坚持中国人的饭碗任何时候都要牢牢端在自己手中,饭碗主要装中国粮.”某粮食生产基地为了落实习近平总书记的重要讲话精神,积极扩大粮食生产规模,计划投入一笔资金购买甲、乙两种农机具,已知 件甲种农机具比 件乙种农机具多 万元,用 万元购买甲种农机具的数量和用 万元购买乙种农机具的数量相同.
(1)求购买 件甲种农机具和 件乙种农机具各需多少万元?
(2)若该粮食生产基地计划购买甲、乙两种农机具共 件,且购买的总费用不超过 万元,则甲种农机具最多能购买多少件?
如图,点 在同一条直线上, .有下列三个条件:① ,② ,③ .
(1)请在上述三个条件中选取一个条件,使得 .
你选取的条件为(填写序号)_____(只需选一个条件,多选不得分),你判定 的依据是_____(填“ ”或“ ”或“ ”或“ ”);
(2)利用(1)的结论 .求证: .
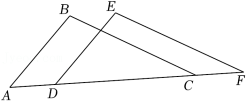
如图,在四边形 中,对角线 与 相交于点 ,记 的面积为 , 的面积为 .
(1)问题解决:如图①,若 ,求证:
(2)探索推广:如图②,若 与 不平行,(1)中的结论是否成立?若成立,请证明;若不成立,请说明理由.
(3)拓展应用:如图③,在 上取一点 ,使 ,过点 作 交 于点 ,点 为 的中点, 交 于点 ,且 ,若 ,求 值.

为实施“乡村振兴”计划,某村产业合作社种植了“千亩桃园”.2022年该村桃子丰收,销售前对本地市场进行调查发现:当批发价为 千元/吨时,每天可售出 吨,每吨涨 千元,每天销量将减少 吨,据测算,每吨平均投入成本 千元,为了抢占市场,薄利多销,该村产业合作社决定,批发价每吨不低于 千元,不高于 千元.请解答以下问题:
(1)求每天销量 (吨)与批发价 (千元/吨)之间的函数关系式,并直接写出自变量 的取值范围;
(2)当批发价定为多少时,每天所获利润最大?最大利润是多少?
如图, 是以 为直径的 上一点,过点 的切线 交 的延长线于点 ,过点 作 交 的延长线于点 ,垂足为点 .
(1)求证: ;
(2)若 , ,求 的长.

为了测量高速公路某桥的桥墩高度,某数学兴趣小组在同一水平地面 两处实地测量,如图所示.在 处测得桥墩顶部 处的仰角为 和桥墩底部 处的俯角为 ,在 处测得桥墩顶部 处的仰角为 ,测得 两点之间的距离为 ,直线 在同一平面内,请你用以上数据,计算桥墩 的高度.(结果保留整数,参考数据: , )
科学规范戴口罩是阻断新冠病毒传播的有效措施之一,某口罩生产厂家接到一公司的订单,生产一段时间后,还剩 万个口罩未生产,厂家因更换设备,生产效率比更换设备前提高了 .结果刚好提前 天完成订单任务.求该厂家更换设备前和更换设备后每天各生产多少万个口罩?
2021年7月,中共中央办公厅,国务院办公厅印发了《关于进一步减轻义务教育阶段学生作业负担和校外培训负担的意见》.某中学为了切实减轻学生作业负担,落实课后服务相关要求,开设了书法、摄影、篮球、足球、乒乓球五项课后服务活动,为了解学生的个性化需求,学校随机抽取了部分学生进行问卷调查,并将调查结果绘制成如图所示的扇形统计图和条形统计图,请你根据给出的信息解答下列问题:

(1)求 的值并把条形统计图补充完整;
(2)若该校有 名学生,试估计该校参加“书法”活动的学生有多少人?
(3)结合调查信息,请你给该校课后服务活动项目开设方面提出一条合理化的建议.
在平面直角坐标系内有三点 .
(1)求过其中两点的直线的函数表达式(选一种情形作答);
(2)判断 三点是否在同一直线上,并说明理由.
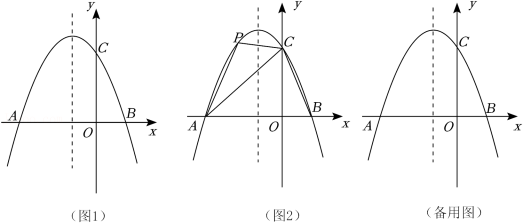
如图1,平面直角坐标系 中,抛物线 与 轴分别交于点 和点 ,与 轴交于点 ,对称轴为直线 ,且 , 为抛物线上一动点.
(1)直接写出抛物线的解析式;
(2)如图2,连接 ,当点 在直线 上方时,求四边形 面积的最大值,并求出此时 点的坐标;
(3)设M为抛物线对称轴上一动点,当 运动时,在坐标轴上是否存在点 ,使四边形 为矩形?若存在,直接写出点 及其对应点 的坐标;若不存在,请说明理由.
《几何原本》是古希腊数学家欧几里得的一部不朽著作,是数学发展史的一个里程碑.在该书的第2卷“几何与代数”部分,记载了很多利用几何图形来论证的代数结论,利用几何给人以强烈印象将抽象的逻辑规律体现在具体的图形之中.
(1)我们在学习许多代数公式时,可以用几何图形来推理,观察下列图形,找出可以推出的代数公式,(下面各图形均满足推导各公式的条件,只需填写对应公式的序号)

公式①:
公式②:
公式③:
公式④:
图1对应公式_____,图2对应公式_____,图3对应公式_____,图4对应公式_____.
(2)《几何原本》中记载了一种利用几何图形证明平方差公式 的方法,如图5,请写出证明过程;(已知图中各四边形均为矩形)
(3)如图6,在等腰直角三角形 中, , 为 的中点, 为边 上任意一点(不与端点重合),过点 作 于点 ,作 于点 ,过点 作 交 的延长线于点 .记 与 的面积之和为 , 与 的面积之和为 .
①若 为边 的中点,则 的值为_____;
②若 不为边 的中点时,试问①中的结论是否仍成立?若成立,写出证明过程;若不成立,请说明理由.
