因疫情防控需要,一辆货车先从甲地出发运送防疫物资到乙地,稍后一辆轿车从甲地急送防疫专家到乙地.已知甲、乙两地的路程是 ,货车行驶时的速度是 .两车离甲地的路程 与时间 的函数图象如图.

(1)求出 的值;
(2)求轿车离甲地的路程 与时间 的函数表达式;
(3)问轿车比货车早多少时间到达乙地?
如图,在 的方格纸中,点 均在格点上,试按要求画出相应格点图形.

(1)如图1,作一条线段,使它是 向右平移一格后的图形;
(2)如图2,作一个轴对称图形,使 和 是它的两条边;
(3)如图3,作一个与 相似的三角形,相似比不等于 .
某校为了解学生在“五•一”小长假期间参与家务劳动的时间 (小时),随机抽取了本校部分学生进行问卷调查.要求抽取的学生在A,B,C,D,E五个选项中选且只选一项,并将抽查结果绘制成如下两幅不完整的统计图,请根据图中信息回答问题:

(1)求所抽取的学生总人数;
(2)若该校共有学生 人,请估算该校学生参与家务劳动的时间满足 的人数;
(3)请你根据调查结果,对该校学生参与家务劳动时间的现状作简短评述.
如图1,四边形 中, , 于点 .将 与该四边形按如图方式放在同一平面内,使点 与 重合,点 在 上,其中 .

(1)求证: ;
(2) 从图1的位置出发,先沿着 方向向右平移(图2),当点 到达点 后立刻绕点 逆时针旋转(图3),当边 旋转 时停止.
①边 从平移开始,到绕点 旋转结束,求边 扫过的面积;
②如图2,点 在 上,且 .若 右移的速度为每秒 个单位长,绕点 旋转的速度为每秒 ,求点 在 区域(含边界)内的时长;
③如图3,在 旋转过程中,设 分别交 于点 ,若 ,直接写出 的长(用含 的式子表示).
如图,平面直角坐标系中,线段 的端点为 .
(1)求 所在直线的解析式;
(2)某同学设计了一个动画:
在函数 中,分别输入 和 的值,使得到射线 ,其中 .当 时,会从C处弹出一个光点 ,并沿 飞行;当 时,只发出射线而无光点弹出.
①若有光点 弹出,试推算 应满足的数量关系;
②当有光点 弹出,并击中线段 上的整点(横、纵坐标都是整数)时,线段 就会发光.求此时整数 的个数.

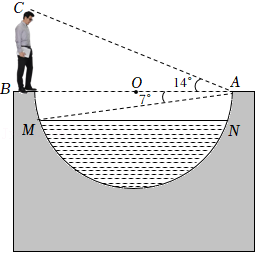
如图,某水渠的横断面是以 为直径的半圆 ,其中水面截线 .嘉琪在 处测得垂直站立于 处的爸爸头顶 的仰角为 ,点 的俯角为 .已知爸爸的身高为 .
(1)求 的大小及 的长;
(2)请在图中画出线段 ,用其长度表示最大水深(不说理由),并求最大水深约为多少米(结果保留小数点后一位).
(参考数据: 取 , 取 )
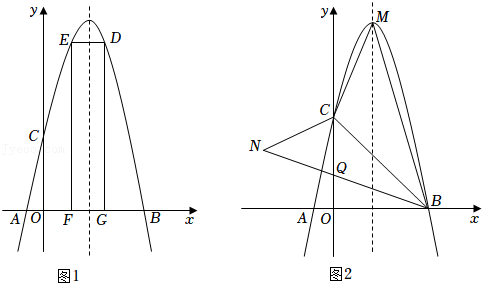
如图,点 在抛物线 上,且在 的对称轴右侧.
(1)写出 的对称轴和 的最大值,并求 的值;
(2)坐标平面上放置一透明胶片,并在胶片上描画出点 及 的一段,分别记为 .平移该胶片,使 所在抛物线对应的函数恰为 .求点 移动的最短路程.

发现两个已知正整数之和与这两个正整数之差的平方和一定是偶数,且该偶数的一半也可以表示为两个正整数的平方和.
验证 如, 为偶数.请把 的一半表示为两个正整数的平方和;
探究 设“发现”中的两个已知正整数为 ,请论证“发现”中的结论正确.
某公司要在甲、乙两人中招聘一名职员,对两人的学历,能力、经验这三项进行了测试.各项满分均为 分,成绩高者被录用.图1是甲、乙测试成绩的条形统计图,
(1)分别求出甲、乙三项成绩之和,并指出会录用谁;
(2)若将甲、乙的三项测试成绩,按照扇形统计图(图2)各项所占之比,分别计算两人各自的综合成绩,并判断是否会改变(1)的录用结果.

已知抛物线 与 轴交于 两点,与 轴交于点 .
(1)求 的值;
(2)如图1,点 是抛物线上位于对称轴右侧的一个动点,且点 在第一象限内,过点 作 轴的平行线交抛物线于点 ,作 轴的平行线交 轴于点 ,过点 作 轴,垂足为点 ,当四边形 的周长最大时,求点 的坐标;
(3)如图2,点 是抛物线的顶点,将 沿 翻折得到 , 与 轴交于点 ,在对称轴上找一点 ,使得 是以 为直角边的直角三角形,求出所有符合条件的点 的坐标.
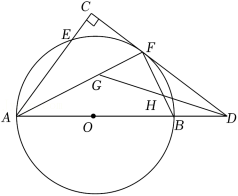
如图,已知 是 的直径,点 是 上异于 的点,点 是 的中点,连接 ,过点 作 交 的延长线于点 ,交 的延长线于点 , 的平分线 交 于点 ,交 于点 .
(1)求证: 是 的切线;
(2)求 的值;
(3)若 , ,求 的直径.