综合运用
如图1,在平面直角坐标系中,正方形 的顶点 在 轴的正半轴上.如图2,将正方形 绕点 逆时针旋转,旋转角为 , 交直线 于点 , 交 轴于点 .
(1)当旋转角 为多少度时, ;(直接写出结果,不要求写解答过程)
(2)若点 ,求 的长;
(3)如图3,对角线 交 轴于点 ,交直线 于点 ,连接 .将 与 的面积分别记为 与 .设 , ,求 关于 的函数表达式.
综合运用
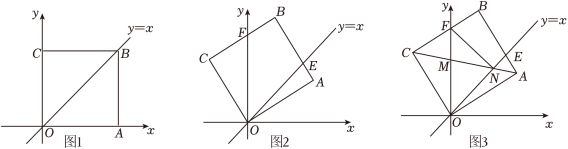
如图1,在平面直角坐标系中,正方形 的顶点 在 轴的正半轴上.如图2,将正方形 绕点 逆时针旋转,旋转角为 , 交直线 于点 , 交 轴于点 .
(1)当旋转角 为多少度时, ;(直接写出结果,不要求写解答过程)
(2)若点 ,求 的长;
(3)如图3,对角线 交 轴于点 ,交直线 于点 ,连接 .将 与 的面积分别记为 与 .设 , ,求 关于 的函数表达式.
