【观察思考】
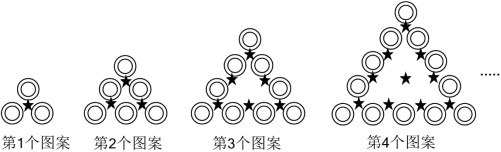
【规律发现】
请用含 的式子填空:
(1)第 个图案中“◎”的个数为_____;
(2)第1个图案中“★”的个数可表示为 ,第 个图案中“★”的个数可表示为 ,第 个图案中“★”的个数可表示为 ,第 个图案中“★”的个数可表示为 ,……,第 个图案中“★”的个数可表示为_____.
【规律应用】
(3)结合图案中“★”的排列方式及上述规律,求正整数 ,使得连续的正整数之和 等于第 个图案中“◎”的个数的 倍.
【观察思考】

【规律发现】
请用含 的式子填空:
(1)第 个图案中“◎”的个数为_____;
(2)第1个图案中“★”的个数可表示为 ,第 个图案中“★”的个数可表示为 ,第 个图案中“★”的个数可表示为 ,第 个图案中“★”的个数可表示为 ,……,第 个图案中“★”的个数可表示为_____.
【规律应用】
(3)结合图案中“★”的排列方式及上述规律,求正整数 ,使得连续的正整数之和 等于第 个图案中“◎”的个数的 倍.