初中数学解答题

抛掷一枚质地均匀的普通硬币，仅有两种可能的结果：“出现正面”或“出现反面”，正面朝上记2分，反面朝上记1分．小明抛掷这枚硬币两次，用画树状图（或列表）的方法，求两次分数之和不大于3的概率．

在四边形ABCD中，O是边BC上的一点．若 $△OAB≌△OCD$，则点O叫做该四边形的“等形点”．

（1）正方形 　 　“等形点”（填“存在”或“不存在”）；

（2）如图，在四边形ABCD中，边BC上的点O是四边形ABCD的“等形点”．已知 $CD＝4\sqrt{2}$， $OA＝5$， $BC＝12$，连接AC，求AC的长；

（3）在四边形EFGH中，EH∥FG．若边FG上的点O是四边形EFGH的“等形点”，求 $\frac{\mathit{OF}}{\mathit{OG}}$的值．

第十四届国际数学教育大会（ICME﹣14）会徽的主题图案有着丰富的数学元素，展现了我国古代数学的文化魅力，其右下方的“卦”是用我国古代的计数符号写出的八进制数3745．八进制是以8作为进位基数的数字系统，有0～7共8个基本数字．八进制数3745换算成十进制数是3×8³+7×8²+4×8¹+5×8⁰＝2021，表示ICME﹣14的举办年份．

（1）八进制数3746换算成十进制数是 　 　；

（2）小华设计了一个n进制数143，换算成十进制数是120，求n的值．

如图，点A在射线OX上，OA＝a．如果OA绕点O按逆时针方向旋转n°（0＜n≤360）到OA′，那么点A′的位置可以用（a，n°）表示．

（1）按上述表示方法，若a＝3，n＝37，则点A′的位置可以表示为 　 　；

（2）在（1）的条件下，已知点B的位置用（3，74°）表示，连接A′A、A′B．求证：A′A＝A′B．

如图，在平面直角坐标系xOy中，一次函数 $y＝2x+b$的图象分别与x轴、y轴交于点A、B，与反比例函数 $y=\frac{k}{x}$（x＞0）的图象交于点C，连接OC．已知点B（0，4），△BOC的面积是2．

（1）求b、k的值；

（2）求△AOC的面积．

在5张相同的小纸条上，分别写有语句：①函数表达式为y＝x；②函数表达式为y＝x²；③函数的图象关于原点对称；④函数的图象关于y轴对称；⑤函数值y随自变量x增大而增大．将这5张小纸条做成5支签，①、②放在不透明的盒子A中搅匀，③、④、⑤放在不透明的盒子B中搅匀．

（1）从盒子A中任意抽出1支签，抽到①的概率是 　 　；

（2）先从盒子A中任意抽出1支签，再从盒子B中任意抽出1支签．求抽到的2张小纸条上的语句对函数的描述相符合的概率．

为减少传统塑料袋对生态环境的破坏，国家提倡使用可以在自然环境下（特定微生物、温度、湿度）较快完成降解的环保塑料袋．调查小组就某小区每户家庭1周内环保塑料袋的使用情况进行了抽样调查，使用情况为A（不使用）、B（1～3个）、C（4～6个）、D（7个及以上），以下是根据调查结果绘制的统计图的一部分．

（1）本次调查的样本容量是 　 　，请补全条形统计图；

（2）已知该小区有1500户家庭，调查小组估计：该小区1周内使用7个及以上环保塑料袋的家庭约有225户．调查小组的估计是否合理？请说明理由．

已知 $\angle MON＝\alpha$，点A，B分别在射线OM，ON上运动，AB＝6．

（1）如图①，若 $\alpha ＝90°$，取AB中点D，点A，B运动时，点D也随之运动，点A，B，D的对应点分别为A′，B′，D′，连接OD，OD′．判断OD与OD′有什么数量关系？证明你的结论；

（2）如图②，若 $\alpha ＝60°$，以AB为斜边在其右侧作等腰直角三角形ABC，求点O与点C的最大距离；

（3）如图③，若 $\alpha ＝45°$，当点A，B运动到什么位置时，△AOB的面积最大？请说明理由，并求出△AOB面积的最大值．

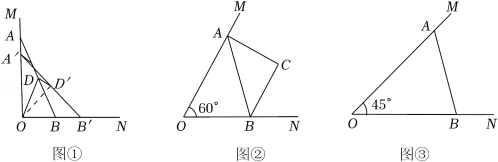
已知抛物线y＝﹣x²+2x+3与x轴交于A，B两点（点A在点B的左侧）．

（1）求点A，点B的坐标；

（2）如图，过点A的直线l：y＝﹣x﹣1与抛物线的另一个交点为C，点P为抛物线对称轴上的一点，连接PA，PC，设点P的纵坐标为m，当PA＝PC时，求m的值；

（3）将线段AB先向右平移1个单位长度，再向上平移5个单位长度，得到线段MN，若抛物线y＝a（﹣x²+2x+3）（a≠0）与线段MN只有一个交点，请直接写出a的取值范围．

如图，在 $△ABC$中， $AB＝AC$，以AC为直径作⊙O交BC于点D，过点D作 $DE\perp AB$，垂足为E，延长BA交⊙O于点F．

（1）求证：DE是⊙O的切线；

（2）若 $\frac{\mathit{AE}}{\mathit{DE}}=\frac{2}{3}$， $AF＝10$，求 $\odot O$的半径．

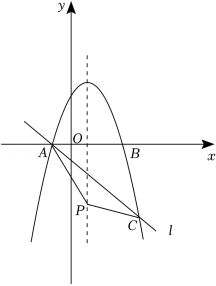
打油茶是广西少数民族特有的一种民俗．某特产公司近期销售一种盒装油茶，每盒的成本价为50元，经市场调研发现，该种油茶的月销售量y（盒）与销售单价x（元）之间的函数图象如图所示．

（1）求y与x的函数解析式，并写出自变量x的取值范围；

（2）当销售单价定为多少元时，该种油茶的月销售利润最大？求出最大利润．

综合与实践

【问题情境】数学活动课上，老师带领同学们开展“利用树叶的特征对树木进行分类”的实践活动．

【实践发现】同学们随机收集芒果树、荔枝树的树叶各10片，通过测量得到这些树叶的长y（单位：cm），宽x（单位：cm）的数据后，分别计算长宽比，整理数据如下：

	1	2	3	4	5	6	7	8	9	10
芒果树叶的长宽比	3.8	3.7	3.5	3.4	3.8	4.0	3.6	4.0	3.6	4.0
荔枝树叶的长宽比	2.0	2.0	2.0	2.4	1.8	1.9	1.8	2.0	1.3	1.9

【实践探究】分析数据如下：

	平均数	中位数	众数	方差
芒果树叶的长宽比	3.74	m	4.0	0.0424
荔枝树叶的长宽比	1.91	1.95	n	0.0669

【问题解决】

（1）上述表格中：m＝　 　，n＝　 　；

（2）①A同学说：“从树叶的长宽比的方差来看，我认为芒果树叶的形状差别大．”

②B同学说：“从树叶的长宽比的平均数、中位数和众数来看，我发现荔枝树叶的长约为宽的两倍．”

上面两位同学的说法中，合理的是 　　（填序号）；

（3）现有一片长11cm，宽5.6cm的树叶，请判断这片树叶更可能来自于芒果、荔枝中的哪种树？并给出你的理由．

如图，在 $▱ABCD$中，BD是它的一条对角线．

（1）求证： $△ABD≌△CDB$；

（2）尺规作图：作BD的垂直平分线EF，分别交AD，BC于点E，F（不写作法，保留作图痕迹）；

（3）连接BE，若 $\angle DBE＝25°$，求 $\angle AEB$的度数．

如图， $AB$为 $\odot O$的直径， $C$是 $\odot O$上一点，过点 $C$的直线交 $AB$的延长线于点 $M$，作 $AD\perp MC$，垂足为 $D$，已知 $AC$平分 $\angle MAD$．

（1）求证： $MC$是 $\odot O$的切线；

（2）若 $AB＝BM＝4$，求 $\tan \angle MAC$的值．

金鹰酒店有 $140$间客房需安装空调，承包给甲、乙两个工程队合作安装，每间客房都安装同一品牌同样规格的一台空调，已知甲工程队每天比乙工程队多安装 $5$台，甲工程队的安装任务有 $80$台，两队同时安装．问：

（1）甲、乙两个工程队每天各安装多少台空调，才能同时完成任务？

（2）金鹰酒店响应“绿色环保”要求，空调的最低温度设定不低于 $26℃$，每台空调每小时耗电 $1.5$度；据预估，每天至少有 $100$间客房有旅客住宿，旅客住宿时平均每天开空调约 $8$小时．若电费 $0.8$元/度，请你估计该酒店每天所有客房空调所用电费 $W$（单位：元）的范围？