如图, 已知直线 与拋物线 交于 两点.
(1)求 两点的坐标;
(2)求线段 的垂直平分线的解析式;
(3)取与线段AB等长的一根橡皮筋,端点分别固定在A,B两处,用铅笔拉着这根橡皮筋使笔尖 在直线 上方的抛物线上移动,动点 将与 构成无数个三角形,这些三角形中是否存在一个面积最大的三角形?如果存在,求出最大面积,并指出此时点 的坐标;如果不存在,请简要说明理由.
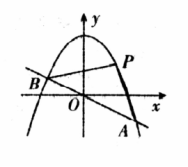
如图, 已知直线 与拋物线 交于 两点.
(1)求 两点的坐标;
(2)求线段 的垂直平分线的解析式;
(3)取与线段AB等长的一根橡皮筋,端点分别固定在A,B两处,用铅笔拉着这根橡皮筋使笔尖 在直线 上方的抛物线上移动,动点 将与 构成无数个三角形,这些三角形中是否存在一个面积最大的三角形?如果存在,求出最大面积,并指出此时点 的坐标;如果不存在,请简要说明理由.
