如图,已知直线 ,与 轴交于点 ,与 轴交于点 ,以 为直径的 交 于另一点 ,把弧 沿直线 翻转后与 交于点 .
(1)当 时,求 的长;
(2)是否存在实数 ,使沿直线 把弧 翻转后所得的弧与 相切?若存在,请求出此时 的值;若不存在,请说明理由.
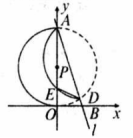
如图,已知直线 ,与 轴交于点 ,与 轴交于点 ,以 为直径的 交 于另一点 ,把弧 沿直线 翻转后与 交于点 .
(1)当 时,求 的长;
(2)是否存在实数 ,使沿直线 把弧 翻转后所得的弧与 相切?若存在,请求出此时 的值;若不存在,请说明理由.
