“无字证明”(proofs without words), 就是将数学命题用简单、有创意而且易于理解的几何图形来呈现.请利用图甲、图乙中阴影部分的面积关系,写出该图所验证的一个三角恒等变换公式: .

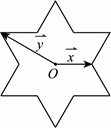
将一圆的六个等分点分成两组相间的三点﹐它们所构成的两个正三角形扣除内部六条线段后可以形成一正六角星﹐如图所示的正六角星是以原点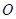 为中心﹐其中
为中心﹐其中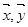 ,分别为原点
,分别为原点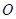 到两个顶点的向量﹒若将原点
到两个顶点的向量﹒若将原点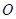 到正六角星12个顶点的向量﹐都写成为
到正六角星12个顶点的向量﹐都写成为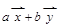 的形式﹐则
的形式﹐则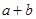 的最大值为( )
的最大值为( )
| A.2 | B.3 | C.4 | D.5 |
(本小题满分13分)已知数列 满足:
满足: ,数列
,数列 满足:
满足: ,
, ,数列
,数列 的前
的前 项和为
项和为 .
.
(Ⅰ)求证:数列 为等比数列;
为等比数列;
(Ⅱ)求证:数列 为递增数列;
为递增数列;
(Ⅲ)若当且仅当 时,
时, 取得最小值,求
取得最小值,求 的取值范围.
的取值范围.
(本小题满分14分)若数列 的各项均为正数,
的各项均为正数, ,
, 为常数,且
为常数,且 .
.
(1)求 的值;
的值;
(2)证明:数列 为等差数列;
为等差数列;
(3)若 ,对任意给定的k∈N*,是否存在p,r∈N*(k<p<r)使
,对任意给定的k∈N*,是否存在p,r∈N*(k<p<r)使 ,
, ,
, 成等差数列?若存在,用k分别表示一组p和r;若不存在,请说明理由.
成等差数列?若存在,用k分别表示一组p和r;若不存在,请说明理由.
(本小题满分12分)已知函数 (其中
(其中 为常数且
为常数且 )在
)在 处取得极值.
处取得极值.
(I) 当 时,求
时,求 的单调区间;
的单调区间;
(II) 若 在
在 上的最大值为
上的最大值为 ,求
,求 的值.
的值.
本题共3个小题,第1小题满分3分,第2小题满分7分,第3小题满分8分.
已知数列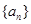 ,
,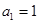 ,
,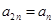 ,
,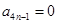 ,
,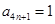
 .
.
(Ⅰ)求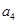 ,
, ;
;
(Ⅱ)是否存在正整数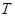 ,使得对任意的
,使得对任意的 ,有
,有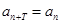 ;
;
(Ⅲ)设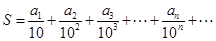 ,问
,问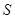 是否为有理数,说明理由.
是否为有理数,说明理由.
(本小题满分12分)设函数 ,
, .
.
(1)解方程: ;
;
(2)令 ,求证:
,求证: ;
;
(3)若 是实数集
是实数集 上的奇函数,且
上的奇函数,且 对任意实数
对任意实数 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(参考公式:当a>0,b>0时, ,当且仅当a=b时等号成立)
,当且仅当a=b时等号成立)
(本小题满分14分)已知函数 是奇函数,且满足
是奇函数,且满足
(1)求实数 、
、 的值;
的值;
(2)试证明函数 在区间
在区间 单调递减,在区间
单调递减,在区间 单调递增;
单调递增;
(3)是否存在实数 同时满足以下两个条件:
同时满足以下两个条件:
①不等式 对
对 恒成立;②方程
恒成立;②方程 在
在 上有解.
上有解.
若存在,试求出实数 的取值范围,若不存在,请说明理由.
的取值范围,若不存在,请说明理由.
(本小题满分14分) 在平面直角坐标系 中,已知圆
中,已知圆 过坐标原点O且圆心在曲线
过坐标原点O且圆心在曲线 上.
上.
(1)若圆M分别与 轴、
轴、 轴交于点
轴交于点 、
、 (不同于原点O),求证:
(不同于原点O),求证: 的面积为定值;
的面积为定值;
(2)设直线 与圆M 交于不同的两点C,D,且
与圆M 交于不同的两点C,D,且 ,求圆M的方程;
,求圆M的方程;
(3)设直线 与(2)中所求圆M交于点
与(2)中所求圆M交于点 、
、 ,
,  为直线
为直线 上的动点,直线
上的动点,直线 ,
, 与圆M的另一个交点分别为
与圆M的另一个交点分别为 ,
, ,求证:直线
,求证:直线 过定点.
过定点.
在数列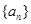 和
和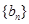 中,
中,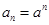 ,
,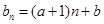 ,
,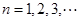 ,其中
,其中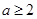 且
且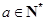 ,
,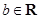 .
.
(Ⅰ)若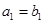 ,
,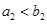 ,求数列
,求数列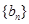 的前
的前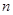 项和;
项和;
(Ⅱ)证明:当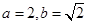 时,数列
时,数列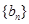 中的任意三项都不能构成等比数列;
中的任意三项都不能构成等比数列;
(Ⅲ)设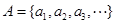 ,
,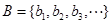 ,试问在区间
,试问在区间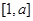 上是否存在实数
上是否存在实数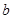 使得
使得 .若存在,求出
.若存在,求出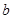 的一切可能的取值及相应的集合
的一切可能的取值及相应的集合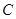 ;若不存在,试说明理由.
;若不存在,试说明理由.
(本小题满分12分)已知函数 满足
满足 ,对任意
,对任意 都有
都有 ,且
,且 .
.
(1)求函数 的解析式;
的解析式;
(2)是否存在实数 ,使函数
,使函数 在
在 上为减函数?若存在,求出实数
上为减函数?若存在,求出实数 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
如图,PA垂直于圆O所在的平面,AB是圆O的直径,C是圆O上的一点,E, F分别是点A在P B, P C上的射影,给出下列结论:
① ;②
;② ;③
;③ ;④
;④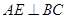 .正确命题的个数为( )
.正确命题的个数为( )
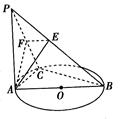
| A.1 | B.2 | C.3 | D.4 |