数列{an}的前n项和为Pn,若 (n∈N*),数列{bn}满足2bn+1=bn+bn+2(n∈N*),且b3=7,b8=22.
(n∈N*),数列{bn}满足2bn+1=bn+bn+2(n∈N*),且b3=7,b8=22.
(1)求数列{an}和{bn}的通项公式an和bn;
(2)设数列cn=anbn,求{cn}的前n项和Sn.
已知函数f(x)= +lnx(a>0)
+lnx(a>0)
(1)若函数f(x)在[1,+∞)上为增函数,求实数a的取值范围;
(2)当a=1时,求f(x)在[ ,2]上的最大值和最小值.
,2]上的最大值和最小值.
已知函数 (
( ).
).
(Ⅰ)当 时,求
时,求 的图象在
的图象在 处的切线方程;
处的切线方程;
(Ⅱ)若函数 在
在 上有两个零点,求实数
上有两个零点,求实数 的取值范围;
的取值范围;
(Ⅲ)若函数 的图象与
的图象与 轴有两个不同的交点
轴有两个不同的交点 ,且
,且 ,
,
求证: (其中
(其中 是
是 的导函数).
的导函数).
已知抛物线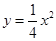 ,过点P(0,2)作直线l,交抛曲线于A,B两点,O为坐标原点,
,过点P(0,2)作直线l,交抛曲线于A,B两点,O为坐标原点,
(Ⅰ)求证: 为定值;
为定值;
(Ⅱ)求三角形AOB面积的最小值.
己知函数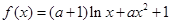
(Ⅰ)讨论函数f(x)的单调性;
(Ⅱ)设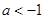 ,若对任意
,若对任意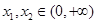 ,恒有
,恒有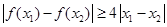 ,求a的取值范围.
,求a的取值范围.
对于函数 ,若存在
,若存在 ,使
,使 成立,则称
成立,则称 为
为 的不动点.已知函数
的不动点.已知函数

 .
.
(1)当 时,求
时,求 的不动点;
的不动点;
(2)若对于任意实数 ,函数
,函数 恒有两个相异的不动点,求
恒有两个相异的不动点,求 的取值范围.
的取值范围.
定义在 上的奇函数
上的奇函数 有最小正周期4,且
有最小正周期4,且 时,
时, .
.
(1)求 在
在 上的解析式;
上的解析式;
(2)判断 在
在 上的单调性,并给予证明;
上的单调性,并给予证明;
(3)当 为何值时,关于方程
为何值时,关于方程 在
在 上有实数解?
上有实数解?
已知函数 .
.
(1)求函数 的最小值;
的最小值;
(2)已知 ,命题
,命题 :关于
:关于 的不等式
的不等式 对任意
对任意 恒成立;
恒成立; :函数
:函数 是增函数.若“
是增函数.若“ 或
或 ”为真,“
”为真,“ 且
且 ”为假,求实数
”为假,求实数 的取值范围.
的取值范围.
为了降低能源损耗,国家对新建住宅的屋顶和外墙都要求建造隔热层,某房地产公司计划采用可使用30年的新型隔热层,已知每厘米厚的隔热层建造成本为8万元,每栋楼房每年的能源消耗费用 (单位:万元)与隔热层厚度
(单位:万元)与隔热层厚度 (单位:cm)满足关系:
(单位:cm)满足关系: ,若不建隔热层,每年能源消耗费用为6万元.设
,若不建隔热层,每年能源消耗费用为6万元.设 为隔热层建造费用与30年的能源消耗费用之和.
为隔热层建造费用与30年的能源消耗费用之和.
(1)求 的值及
的值及 的表达式;
的表达式;
(2)隔热层修建多厚时,总费用 达到最小,并求最小值.
达到最小,并求最小值.