设函数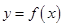 在区间
在区间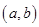 上的导函数为
上的导函数为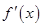 ,
,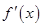 在区间
在区间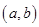 上的导函数为
上的导函数为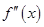 ,若区间
,若区间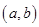 上
上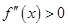 ,则称函数
,则称函数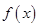 在区间
在区间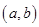 上为“凹函数”,已知
上为“凹函数”,已知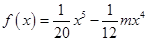
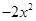 在
在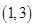 上为“凹函数”,则实数m的取值范围是( )
上为“凹函数”,则实数m的取值范围是( )
A.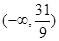 |
B.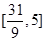 |
C.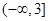 |
D.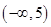 |
已知函数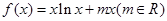 的图象在点
的图象在点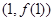 处的切线的斜率为2.
处的切线的斜率为2.
(Ⅰ)求实数 的值;
的值;
(Ⅱ)设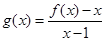 ,讨论
,讨论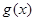 的单调性;
的单调性;
(Ⅲ)已知 且
且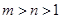 ,证明:
,证明: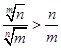 .
.
(本小题12分)已知 分别为椭圆
分别为椭圆 :
: (
( )的左、右焦点, 且离心率为
)的左、右焦点, 且离心率为 ,点
,点 椭圆
椭圆 上
上
(1)求椭圆 的方程;
的方程;
(2)是否存在斜率为 的直线
的直线 与椭圆
与椭圆 交于不同的两点
交于不同的两点 ,使直线
,使直线 与
与 的倾斜角互补,且直线
的倾斜角互补,且直线 是否恒过定点,若存在,求出该定点的坐标;若不存在,说明理由.
是否恒过定点,若存在,求出该定点的坐标;若不存在,说明理由.
(本小题满分12分)已知函数 在区间[2,3]上有最大值4和最小值1,设
在区间[2,3]上有最大值4和最小值1,设
(1)求a、b的值;
(2)若不等式 在
在 上有解,求实数k的取值范围
上有解,求实数k的取值范围
如图,在一个正方体内放入两个半径不相等的球 ,这两个球相外切,且球
,这两个球相外切,且球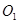 与正方体共顶点A的三个面相切,球
与正方体共顶点A的三个面相切,球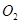 与正方体共顶点
与正方体共顶点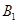 的三个面相切,则两球在正方体的面
的三个面相切,则两球在正方体的面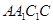 上的正投影是( )
上的正投影是( )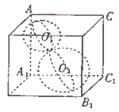

(本小题满分14分)已知函数f(x)=(1-x)ex-1,其中e=2.71828…为自然对数的底数.
(1)求函数f(x)的最大值;
(2)若0≤x<1时,g(x)=ex+λln(1-x)-1≤0,求λ的取值范围;
(3)证明: <n+ln2(n∈N*).
<n+ln2(n∈N*).
(本小题满分14分) 已知椭圆 的中心在原点,焦点在
的中心在原点,焦点在 轴上,离心率等于
轴上,离心率等于 ,它的一个顶点恰好是抛物线
,它的一个顶点恰好是抛物线 的焦点.
的焦点.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)点
 ,
, ,
, 
 ,
, 在椭圆上,
在椭圆上, 、
、 是椭圆上位于直线
是椭圆上位于直线 两侧的动点.
两侧的动点.
①若直线 的斜率为
的斜率为 ,求四边形
,求四边形 面积的最大值;
面积的最大值;
②当 、
、 运动时,满足于
运动时,满足于 ,试问直线
,试问直线 的斜率是否为定值?若是,请求出定值,若不是,请说明理由.
的斜率是否为定值?若是,请求出定值,若不是,请说明理由.
(本小题满分14分)设函数 ,
, 为曲线
为曲线 在点
在点 处的切线.
处的切线.
(Ⅰ)求L的方程;
(Ⅱ)当 时,证明:除切点
时,证明:除切点 之外,曲线C在直线L的下方;
之外,曲线C在直线L的下方;
(Ⅲ)设 ,且满足
,且满足 ,求
,求 的最大值.
的最大值.
(本小题满分14分)已知函数 .
.
(Ⅰ)若 ,求函数
,求函数 的单调递减区间;
的单调递减区间;
(Ⅱ)若 ,求函数
,求函数 在区间
在区间 上的最大值;
上的最大值;
(Ⅲ)若 在区间
在区间 上恒成立,求
上恒成立,求 的最大值.
的最大值.
(本小题满分14分)已知圆 :
: ,直线
,直线 .
.
(1)若直线l与圆 交于不同的两点
交于不同的两点 ,当
,当 时,求
时,求 的值;
的值;
(2)若 ,
, 是直线l上的动点,过
是直线l上的动点,过 作圆
作圆 的两条切线
的两条切线 、
、 ,切点为
,切点为 、
、 ,探究:直线
,探究:直线 是否过定点;
是否过定点;
(3)若 、
、 为圆
为圆 :
: 的两条相互垂直的弦,垂足为
的两条相互垂直的弦,垂足为 ,求四边形
,求四边形 的面积的最大值.
的面积的最大值.
已知数列 是等差数列,其前n项和为Sn,若
是等差数列,其前n项和为Sn,若 ,
, .
.
(1)求 ;
;
(2)若数列{Mn}满足条件:  ,当
,当 时,
时, -
- ,其中数列
,其中数列 单调递增,且
单调递增,且 ,
, .
.
①试找出一组 ,
, ,使得
,使得 ;
;
②证明:对于数列 ,一定存在数列
,一定存在数列 ,使得数列
,使得数列 中的各数均为一个整数的平方.
中的各数均为一个整数的平方.
如图,在平面直角坐标系 中,已知椭圆
中,已知椭圆 :
: ,设
,设 是椭圆
是椭圆 上的任一点,从原点
上的任一点,从原点 向圆
向圆 :
: 作两条切线,分别交椭圆于点
作两条切线,分别交椭圆于点 ,
, .
.
(1)若直线 ,
, 互相垂直,求圆
互相垂直,求圆 的方程;
的方程;
(2)若直线 ,
, 的斜率存在,并记为
的斜率存在,并记为 ,
, ,求证:
,求证: ;
;
(3)试问 是否为定值?若是,求出该值;若不是,说明理由.
是否为定值?若是,求出该值;若不是,说明理由.
已知函数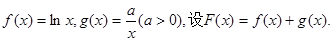
(1)求函数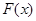 的单调区间;
的单调区间;
(2)若以函数 的图象上任意一点
的图象上任意一点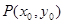 为切点的切线的斜率
为切点的切线的斜率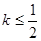 恒成立,求实数a的最小值;
恒成立,求实数a的最小值;
(3)是否存在实数m,使得函数 的图象恰有四个不同的交点?若存在,求出实数m的取值范围;若不存在,请说明理由.
的图象恰有四个不同的交点?若存在,求出实数m的取值范围;若不存在,请说明理由.