已知函数 ,(
,( 为常数,
为常数, 为自然对数的底).
为自然对数的底).
(1)令 ,
, ,求
,求 和
和 ;
;
(2)若函数 在
在 时取得极小值,试确定
时取得极小值,试确定 的取值范围;
的取值范围;
(3)在(2)的条件下,设由 的极大值构成的函数为
的极大值构成的函数为 ,试判断曲线
,试判断曲线 只可能与直线
只可能与直线 、
、 (
( ,
, 为确定的常数)中的哪一条相切,并说明理由.
为确定的常数)中的哪一条相切,并说明理由.
设椭圆 :
: 的离心率为
的离心率为 ,点
,点 (
( ,0),
,0), (0,
(0, ),原点
),原点 到直线
到直线 的距离为
的距离为
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)设点 为(
为( ,0),点
,0),点 在椭圆
在椭圆 上(与
上(与 、
、 均不重合),点
均不重合),点 在直线
在直线 上,若直线
上,若直线 的方程为
的方程为 ,且
,且 ,试求直线
,试求直线 的方程.
的方程.
如图,圆 :
: .
.
(Ⅰ)若圆 与
与 轴相切,求圆
轴相切,求圆 的方程;
的方程;
(Ⅱ)已知 ,圆
,圆 与
与 轴相交于两点
轴相交于两点 (点
(点 在点
在点 的左侧).过点
的左侧).过点 任作一条直线与圆
任作一条直线与圆 :
: 相交于两点
相交于两点 .问:是否存在实数
.问:是否存在实数 ,使得
,使得 ?若存在,求出实数
?若存在,求出实数 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
(本小题14分)如图,已知某椭圆的焦点是 ,过点
,过点 并垂直于x轴的直线与椭圆的一个交点为B,且
并垂直于x轴的直线与椭圆的一个交点为B,且 ,椭圆上不同的两点
,椭圆上不同的两点 满足条件:
满足条件: 、
、 、
、 成等差数列.
成等差数列.

(Ⅰ)求该椭圆的方程;
(Ⅱ)求弦 中点的横坐标;
中点的横坐标;
(Ⅲ)设弦 的垂直平分线的方程为
的垂直平分线的方程为 ,求m的取值范围.
,求m的取值范围.
(本小题满分12分)设 上的两点,已知
上的两点,已知 ,
, ,若
,若 且椭圆的离心率
且椭圆的离心率 短轴长为2,
短轴长为2, 为坐标原点.
为坐标原点.
(Ⅰ)求椭圆的方程;
(Ⅱ)若直线AB过椭圆的焦点F(0,c),(c为半焦距),求直线AB的斜率k的值;(Ⅲ)试问:△AOB的面积是否为定值?如果是,请给予证明;如果不是,请说明理由
圆锥曲线中不同曲线的性质都是有一定联系的,比如圆可以看成特殊的椭圆,所以很多圆的性质结论可以类比到椭圆,例如;如图所示,椭圆C: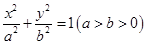 可以被认为由圆
可以被认为由圆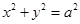 作纵向压缩变换或由圆
作纵向压缩变换或由圆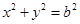 作横向拉伸变换得到的。依据上述论述我们可以推出椭圆C的面积公式为 .
作横向拉伸变换得到的。依据上述论述我们可以推出椭圆C的面积公式为 .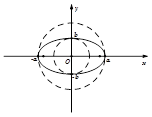
当a>0且x>0时,因为 ,所以
,所以 ,从而
,从而 (当x=
(当x= 时取等号).记函数
时取等号).记函数 ,由上述结论可知:当x=
,由上述结论可知:当x= 时,该函数有最小值为2
时,该函数有最小值为2
(1)已知函数y1=x(x>0)与函数 ,则当x= 时,y1+y2取得最小值为
,则当x= 时,y1+y2取得最小值为
(2)已知函数y1=x+1(x>-1)与函数y2=(x+1)2+4(x>−1),求 的最小值,并指出取得该最小值时相应的x的值.
的最小值,并指出取得该最小值时相应的x的值.
如图,在平面直角坐标系 中,已知椭圆
中,已知椭圆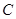 :
: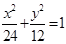 ,设
,设 是椭圆
是椭圆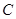 上的任一点,从原点
上的任一点,从原点 向圆
向圆 :
: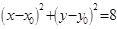 作两条切线,分别交椭圆于点
作两条切线,分别交椭圆于点 ,
, .
.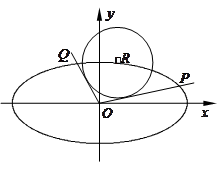
(1)若直线 ,
, 互相垂直,求圆
互相垂直,求圆 的方程;
的方程;
(2)若直线 ,
, 的斜率存在,并记为
的斜率存在,并记为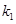 ,
, ,求证:
,求证: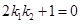 ;
;
(3)试问 是否为定值?若是,求出该值;若不是,说明理由.
是否为定值?若是,求出该值;若不是,说明理由.
(本小题满分13分)已知点 在椭圆
在椭圆 上,椭圆
上,椭圆 的左焦点为(-1,0)
的左焦点为(-1,0)
(1)求椭圆 的方程;
的方程;
(2)直线 过点
过点 交椭圆C于M、N两点,AB是椭圆
交椭圆C于M、N两点,AB是椭圆 经过原点
经过原点 的弦,且MN//AB,问是否存在正数
的弦,且MN//AB,问是否存在正数 ,使
,使 为定值?若存在,求出
为定值?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.