当a>0且x>0时,因为 ,所以
,所以 ,从而
,从而 (当x=
(当x= 时取等号).记函数
时取等号).记函数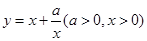 ,由上述结论可知:当x=
,由上述结论可知:当x= 时,该函数有最小值为2
时,该函数有最小值为2
(1)已知函数y1=x(x>0)与函数 ,则当x= 时,y1+y2取得最小值为
,则当x= 时,y1+y2取得最小值为
(2)已知函数y1=x+1(x>-1)与函数y2=(x+1)2+4(x>−1),求 的最小值,并指出取得该最小值时相应的x的值.
的最小值,并指出取得该最小值时相应的x的值.
推荐套卷
当a>0且x>0时,因为 ,所以
,所以 ,从而
,从而 (当x=
(当x= 时取等号).记函数
时取等号).记函数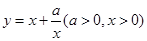 ,由上述结论可知:当x=
,由上述结论可知:当x= 时,该函数有最小值为2
时,该函数有最小值为2
(1)已知函数y1=x(x>0)与函数 ,则当x= 时,y1+y2取得最小值为
,则当x= 时,y1+y2取得最小值为
(2)已知函数y1=x+1(x>-1)与函数y2=(x+1)2+4(x>−1),求 的最小值,并指出取得该最小值时相应的x的值.
的最小值,并指出取得该最小值时相应的x的值.