2019年全国统一高考理科数学试卷(天津卷)
设 ,则" "是" "的( )
| A. |
充分而不必要条件 |
B. |
必要而不充分条件 |
| C. |
充要条件 |
D. |
既不充分也不必要条件 |
已知抛物线
的焦点为
,准线为
,若
与双曲线
的两条渐近线分别交于点 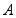 和点
和点  ,且
(
,且
(  为原点),则双曲线的离心率为( )
为原点),则双曲线的离心率为( )
| A. |
|
B. |
|
C. |
|
D. |
|
已知函数 是奇函数,将 的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),所得图象对应的函数为 .若 的最小正周期为 ,且 ,则 ( )
| A. |
|
B. |
|
C. |
|
D. |
|
已知四棱锥的底面是边长为 的正方形,侧棱长均为 .若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点,另一个底面的圆心为四棱锥底面的中心,则该圆柱的体积为_____________.
设甲、乙两位同学上学期间,每天7:30之前到校的概率均为 .假定甲、乙两位同学到校情况互不影响,且任一同学每天到校情况相互独立.
(Ⅰ)用 表示甲同学上学期间的三天中7:30之前到校的天数,求随机变量 的分布列和数学期望;
(Ⅱ)设 为事件“上学期间的三天中,甲同学在7:30之前到校的天数比乙同学在7:30之前到校的天数恰好多2”,求事件 发生的概率.
如图, 平面 , , .
(Ⅰ)求证: 平面 ;
(Ⅱ)求直线 与平面 所成角的正弦值;
(Ⅲ)若二面角 的余弦值为 ,求线段 的长.

设椭圆 的左焦点为 ,上顶点为 .已知椭圆的短轴长为4,离心率为 .
(Ⅰ)求椭圆的方程;
(Ⅱ)设点 在椭圆上,且异于椭圆的上、下顶点,点 为直线 与 轴的交点,点 在 轴的负半轴上.若 ( 为原点),且 ,求直线 的斜率.
设 是等差数列, 是等比数列.已知 .
(Ⅰ)求 和 的通项公式;
(Ⅱ)设数列 满足 其中 .
(i)求数列 的通项公式;
(ii)求 .

 粤公网安备 44130202000953号
粤公网安备 44130202000953号