．(本题满分10分) 选修4—4：坐标系与参数方程
已知曲线Ｃ1的极坐标方程为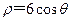
,曲线C2的极坐标方程为
，曲线C1,C2相交于点A、B．
(1)分别将曲线C1，C2的极坐标方程化为直角坐标方程；
(2)求弦AB的长．
，
，试判断
，
所在象限．
皆为锐角，且
，求
的值．
；
．
的定义域．
，求
的值．相关知识点
推荐套卷
．(本题满分10分) 选修4—4：坐标系与参数方程
已知曲线Ｃ1的极坐标方程为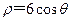,曲线C2的极坐标方程为，曲线C1,C2相交于点A、B．
(1)分别将曲线C1，C2的极坐标方程化为直角坐标方程；
(2)求弦AB的长．
粤公网安备 44130202000953号