定义在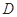 上的函数
上的函数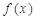 ,如果满足:对任意
,如果满足:对任意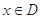 ,存在常数
,存在常数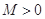 ,都有
,都有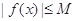 成立,则称
成立,则称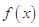 是
是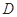 上的有界函数,其中
上的有界函数,其中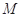 称为函数
称为函数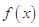 的上界.已知函数
的上界.已知函数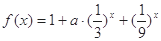 ,
,
(1)当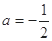 时,求函数
时,求函数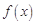 在
在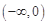 上的值域,并判断函数
上的值域,并判断函数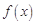 在
在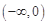 上是否为有界函数,请说明理由;
上是否为有界函数,请说明理由;
(2)若函数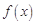 在
在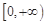 上是以4为上界的有界函数,求实数
上是以4为上界的有界函数,求实数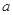 的取值范围.
的取值范围.
已知 是定义在
是定义在 上的奇函数,且
上的奇函数,且 ,若
,若 时,有
时,有
(1)证明 在
在 上是增函数;
上是增函数;
(2)解不等式
(3)若 对
对 恒成立,求实数
恒成立,求实数 的取值范围
的取值范围
已知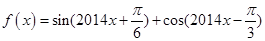 的最大值为
的最大值为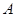 ,若存在实数
,若存在实数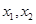 ,使得对任意实数x总有
,使得对任意实数x总有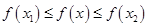 成立,则
成立,则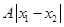 的最小值为( )
的最小值为( )
A.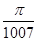 |
B.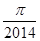 |
C.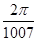 |
D.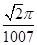 |
设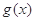 为
为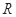 上不恒等于0的奇函数,
上不恒等于0的奇函数,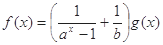 (
(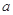 >0且
>0且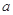 ≠1)为偶函数,则常数
≠1)为偶函数,则常数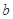 的值为( )
的值为( )
| A.2 | B.1 | C.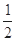 |
D.与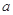 有关的值 有关的值 |
(本小题满分14分)已知函数 ,若在区间
,若在区间 内有且仅有一个
内有且仅有一个 ,使得
,使得 成立,则称函数
成立,则称函数 具有性质
具有性质 .
.
(1)若 ,判断
,判断 是否具有性质
是否具有性质 ,说明理由;
,说明理由;
(2)若函数 具有性质
具有性质 ,试求实数
,试求实数 的取值范围.
的取值范围.
(本小题满分14分)已知数列 中
中 .
. 为实常数.
为实常数.
(Ⅰ)若 ,求数列
,求数列 的通项公式;
的通项公式;
(Ⅱ)若 .
.
①是否存在常数 求出
求出 的值,若不存在,请说明理由;
的值,若不存在,请说明理由;
②设  .证明:n≥2时,
.证明:n≥2时, .
.
(本小题满分12分)已知定义域为 的函数
的函数 满足:
满足:
① 时,
时, ;
;
② ;
;
③对任意的正实数 ,都有
,都有 ;
;
(1)求证: ;
;
(2)求证: 在定义域内为减函数;
在定义域内为减函数;
(3)求不等式 的解集.
的解集.
(本小题满分12分)已知函数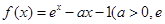 为自然对数的底数)
为自然对数的底数)
(1)求函数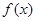 的最小值;
的最小值;
(2)若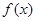 ≥0对任意的x∈R恒成立,求实数a的值;
≥0对任意的x∈R恒成立,求实数a的值;
(3)在(2)的条件下,证明: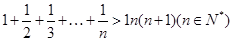
函数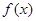 的定义域为
的定义域为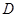 ,若满足:
,若满足:
①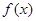 在
在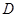 内是单调函数;
内是单调函数;
②存在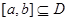 ,使
,使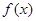 在
在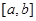 上的值域为
上的值域为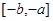 ,那么
,那么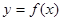 叫做对称函数.
叫做对称函数.
现有 是对称函数,那么
是对称函数,那么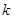 的取值范围是( )
的取值范围是( )
A.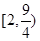 |
B.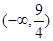 |
C.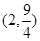 |
D.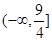 |
已知 分别是椭圆
分别是椭圆 的左、右焦点,椭圆
的左、右焦点,椭圆 过点
过点 且与抛物线
且与抛物线 有一个公共的焦点.
有一个公共的焦点.
(1)求椭圆 方程;
方程;
(2)直线 过椭圆
过椭圆 的右焦点
的右焦点 且斜率为
且斜率为 与椭圆
与椭圆 交于
交于 两点,求弦
两点,求弦 的长;
的长;
(3)以第(2)题中的 为边作一个等边三角形
为边作一个等边三角形 ,求点
,求点 的坐标.
的坐标.
已知椭圆 的离心率为
的离心率为 ,且过点
,且过点

(1)求椭圆的标准方程:
(2)四边形ABCD的顶点在椭圆上,且对角线AC,BD过原点O,若
①求 的最值:
的最值:
②求证:四边形ABCD的面积为定值.