暖春三月,贴心开学测 高三数学第三套
如图,EFGH是以O为圆心,1为半径的圆的内接正方形,将一颗豆子随机地掷到圆内,用A表示事件“豆子落在正方形EFGH内”,B表示事件“豆子落在扇形HOE(阴影部分)内”,则P(B|A)=( )

A. B.
B. C.
C. D.
D.
已知函数 在[-5,5]上是偶函数,且在[0,5]上是单调函数,满足
在[-5,5]上是偶函数,且在[0,5]上是单调函数,满足 ,则下列不等式一定成立的是( )
,则下列不等式一定成立的是( )
A. |
B. |
C. |
D. |
要得到函数 的图象,只需将函数
的图象,只需将函数 的图象上所有的点( )
的图象上所有的点( )
A.横坐标伸长到原的2倍(纵坐标不变),再向右平行移动 个单位长度 个单位长度 |
B.横坐标缩短到原的 倍(纵坐标不变),再向左平行移动 倍(纵坐标不变),再向左平行移动 个单位长度 个单位长度 |
C.横坐标缩短到原的 倍(纵坐标不变),再向右平行移动 倍(纵坐标不变),再向右平行移动 个单位长度 个单位长度 |
D.横坐标伸长到原的2倍(纵坐标不变),再向左平行移动 个单位长度 个单位长度 |
设长方形ABCD边长分别是AD=1,AB=2(如图所示),点P在 BCD内部和边界上运动,设
BCD内部和边界上运动,设 (
( 都是实数),则
都是实数),则 的取值范围是( )
的取值范围是( )

| A.[1,2] | B.[1,3] | C.[2,3] | D.[0,2] |
已知  ABC的三个顶点在以
ABC的三个顶点在以 为球心的球面上,且
为球心的球面上,且  ,BC=1,AC=3,三棱锥
,BC=1,AC=3,三棱锥 的体积为
的体积为  ,则球
,则球 的表面积为__________.
的表面积为__________.
(选修4-1:几何证明选讲)如图, 是圆
是圆 的切线,切点为点
的切线,切点为点 ,直线
,直线 与圆
与圆 交于
交于 、
、 两点,
两点, 的角平分线交弦
的角平分线交弦 、
、 于
于 、
、 两点,已知
两点,已知 ,
, ,则
,则 的值为 .
的值为 .

(本小题满分12分)李明在10场篮球比赛中的投篮情况统计如下(假设各场比赛相互独立):
| 场次 |
投篮次数 |
命中次数 |
场次 |
投篮次数 |
命中次数 |
| 主场1 |
22 |
12 |
客场1 |
18 |
8 |
| 主场2 |
15 |
12 |
客场2 |
13 |
12 |
| 主场3 |
12 |
8 |
客场3 |
21 |
7 |
| 主场4 |
23 |
8 |
客场4 |
18 |
15 |
| 主场5 |
24 |
20 |
客场5 |
25 |
12 |
(1)从上述比赛中随机选择一场,求李明在该场比赛中投篮命中率超过0.6的概率;
(2)从上述比赛中随机选择一个主场和一个客场,求李明的投篮命中率一场超过0.6,一场不超过0.6的概率;
(3)记 为表中10个命中次数的平均数,从上述比赛中随机选择一场,记
为表中10个命中次数的平均数,从上述比赛中随机选择一场,记 为李明在这场比赛中的命中次数,比较
为李明在这场比赛中的命中次数,比较 与
与 的大小(只需写出结论)
的大小(只需写出结论)
(本题满分12分)如图,四边形PDCE为矩形,ABCD为梯形,平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD= CD=1,PD=
CD=1,PD= .
.
(1)若M为PA中点,求证:AC∥平面MDE;
(2)求直线PA与平面PBC所成角的正弦值;
(3)在线段PC上是否存在一点Q(除去端点),使得平面QAD与平面PBC所成锐二面角的大小为 ?
?
(本小题满分13分)已知函数 .
.
(1)求函数 的最大值;
的最大值;
(2)若函数 与
与 有相同极值点,
有相同极值点,
(ⅰ)求实数 的值;
的值;
(ⅱ)若对于 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(本小题满分13分)已知椭圆 :
: (
( )的焦距为
)的焦距为 ,且过点
,且过点 .
.
(1)求椭圆 的方程和离心率;
的方程和离心率;
(2)设 (
( )为椭圆
)为椭圆 上一点,过点
上一点,过点 作
作 轴的垂线,垂足为
轴的垂线,垂足为 .取点
.取点 ,连 结
,连 结 ,过点
,过点 作
作 的垂线交
的垂线交 轴于点
轴于点 ,点
,点 是点
是点 关于
关于 轴的对称点.试判断直线
轴的对称点.试判断直线 与椭圆
与椭圆 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.
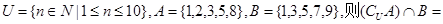 ( )
( )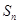 为等比数列
为等比数列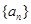 的前n项和,
的前n项和,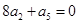 ,则
,则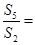 ( )
( ) ,则输出的
,则输出的 属于( )
属于( )




 与直线
与直线 平行,则它们之间的距离为( )
平行,则它们之间的距离为( )



 ,
, ,
, ,且
,且 ,那么
,那么 与
与 的夹角为( )
的夹角为( )



 ,若在圆
,若在圆 上存在点N,使得
上存在点N,使得 ,则
,则 的取值范围是( )
的取值范围是( )



 ,则在复平面内,复数
,则在复平面内,复数 对应的点位于第 象限.
对应的点位于第 象限.  的最小值为_____________.
的最小值为_____________.
 行
行 从左向右的第3个数为
从左向右的第3个数为  (
( 为参数)相交于
为参数)相交于 、
、 两点,则|
两点,则| |= .
|= . 中,角
中,角 的对边分别为
的对边分别为 ,
, ,
,
 .
. 的值;(Ⅱ)求
的值;(Ⅱ)求 的值.
的值. 的前
的前 项和为
项和为 ,已知
,已知 ,
, ,
, .
. .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号