(本小题满分12分)已知抛物线 的焦点为
的焦点为 ,过点
,过点 作一条直线
作一条直线 与抛物线交于
与抛物线交于 ,
, 两点.
两点.
(Ⅰ)求以点 为圆心,且与直线
为圆心,且与直线 相切的圆的方程;
相切的圆的方程;
(Ⅱ)从 中取出三个量,使其构成等比数列,并予以证明.
中取出三个量,使其构成等比数列,并予以证明.
(本小题满分12分)“ALS冰桶挑战赛”是一项社交网络上发起的筹款活动,活动规定:被邀请者要么在24小时内接受挑战,要么选择为慈善机构捐款(不接受挑战),并且不能重复参加该活动.若被邀请者接受挑战,则他需在网络上发布自己被冰水浇遍全身的视频内容,然后便可以邀请另外3个人参与这项活动.假设每个人接受挑战与不接受挑战是等可能的,且互不影响.
(Ⅰ)若某参与者接受挑战后,对其他3个人发出邀请,则这3个人中至少有2个人接受挑战的概率是多少?
(Ⅱ)为了解冰桶挑战赛与受邀者的性别是否有关,某调查机构进行了随机抽样调查,调查得到如下 列联表:
列联表:
| |
接受挑战 |
不接受挑战 |
合计 |
| 男性 |
45 |
15 |
60 |
| 女性 |
25 |
15 |
40 |
| 合计 |
70 |
30 |
100 |
根据表中数据,能否在犯错误的概率不超过 的前提下认为“冰桶挑战赛与受邀者的性别有关”?
的前提下认为“冰桶挑战赛与受邀者的性别有关”?
附:
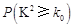 |
0.100 |
0.050 |
0.010 |
0.001 |
 |
2.706 |
3.841 |
6.635 |
10.828 |
如图,在直角梯形ABCD中,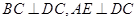 ,M、N分别是AD、AE的中点,将三角形ADE沿AE折起,下列说法正确的是 (填上所有正确的序号)。
,M、N分别是AD、AE的中点,将三角形ADE沿AE折起,下列说法正确的是 (填上所有正确的序号)。
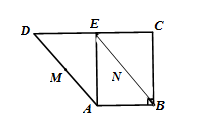
①不论D折至何位置(不在平面ABC内)都有 ;
;
②不论D折至何位置都有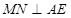 ;
;
③不论D折至何位置(不在平面ABC内)都有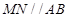 ;
;
④在折起过程中,一定存在某个位置,使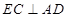 。
。
(理科做)如图所示,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F且EF=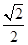 ,则下列结论中错误的是 ( ).
,则下列结论中错误的是 ( ).
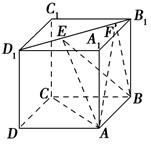
A.AC⊥BE
B.EF∥平面ABCD
C.三棱锥A-BEF的体积为定值
D.异面直线AE,BF所成的角为定值
(文科做)对于三次函数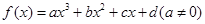 ,给出定义:设
,给出定义:设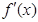 是函数
是函数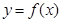 的导数,
的导数,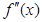 是
是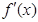 的导数,若方程
的导数,若方程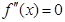 有实数解
有实数解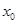 ,则称点
,则称点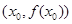 为函数
为函数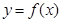 的“拐点”.经过探究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且“拐点”就是对称中心.设函数
的“拐点”.经过探究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且“拐点”就是对称中心.设函数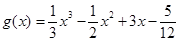 ,则
,则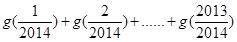 =( )
=( )
A.2011 B.2012 C.2013 D.2014
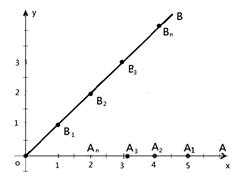
(本题满分14分,第1小题4分,第2小题5分,第3小题5分)平面直角坐标系中, 为原点,射线
为原点,射线 与
与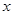 轴正半轴重合,射线
轴正半轴重合,射线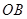 是第一象限角平分线.在
是第一象限角平分线.在 上有点列
上有点列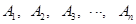 ,
,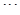 ,在
,在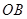 上有点列
上有点列 ,
,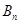 ,
,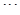 .已知
.已知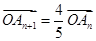 ,
,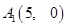 ,
,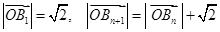 .
.
(1)求点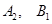 的坐标;
的坐标;
(2)求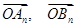 的坐标;
的坐标;
(3)求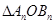 面积的最大值,并说明理由.
面积的最大值,并说明理由.
(本小题满分12分)已知椭圆 的离心率为
的离心率为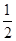 ,直线
,直线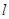 过点
过点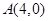 ,
, ,且与椭圆
,且与椭圆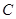 相切于点
相切于点 .
.
(1)求椭圆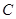 的方程;
的方程;
(2)是否存在过点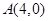 的直线
的直线 与椭圆
与椭圆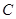 相交于不同的两点
相交于不同的两点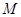 、
、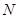 ,使得
,使得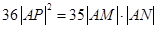 ?若存在,试求出直线
?若存在,试求出直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
已知椭圆 经过点
经过点 ,离心率为
,离心率为 .
.
(1)求椭圆 的方程;
的方程;
(2)直线 与椭圆
与椭圆 交于
交于 两点,点
两点,点 是椭圆
是椭圆 的右顶点.直线
的右顶点.直线 与直线
与直线 分别与
分别与 轴交于点
轴交于点 ,试问以线段
,试问以线段 为直径的圆是否过
为直径的圆是否过 轴上的定点?若是,求出定点坐标;若不是,说明理由.
轴上的定点?若是,求出定点坐标;若不是,说明理由.
已知椭圆 =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e= ,过点A(0,-b)和B(a,0)的直线与坐标原点距离为
,过点A(0,-b)和B(a,0)的直线与坐标原点距离为 .
.
(1)求椭圆的方程;
(2)已知定点E(-1,0),若直线y=kx+2(k≠0)与椭圆相交于C、D两点,试判断是否存在k值,使以CD为直径的圆过定点E?若存在求出这个k值,若不存在说明理由.
已知椭圆C: 的两焦点与短轴的一个端点的连线构成等腰直角三角形,直线
的两焦点与短轴的一个端点的连线构成等腰直角三角形,直线 与以椭圆C的右焦点为圆心,以
与以椭圆C的右焦点为圆心,以
 为半径的圆相切.
为半径的圆相切.
(1)求椭圆的方程.
(2)若过椭圆 的右焦点
的右焦点 作直线
作直线 交椭圆
交椭圆 于
于 两点,交y轴于
两点,交y轴于 点,且
点,且 求证:
求证: 为定值
为定值
(本小題满分16分)已知椭圆 :
: 的焦距为
的焦距为 ,离心率为
,离心率为 ,其右焦点为
,其右焦点为 ,过点
,过点 作直线交椭圆于另一点
作直线交椭圆于另一点 .
.
(1)若 ,求
,求 外接圆的方程;
外接圆的方程;
(2)若过点 的直线与椭圆
的直线与椭圆
 相交于两点
相交于两点 、
、 ,设
,设 为
为 上一点,且满足
上一点,且满足 (
( 为坐标原点),当
为坐标原点),当 时,求实数
时,求实数 的取值范围.
的取值范围.
(本小题满分12分)设 上的两点,已知向量
上的两点,已知向量 ,
, ,若
,若 且椭圆的离心率
且椭圆的离心率 短轴长为2,
短轴长为2, 为 坐标原点.
为 坐标原点.
(Ⅰ)求椭圆的方程;
(Ⅱ)若直线 过椭圆的焦点
过椭圆的焦点 (0,c),(c为半焦距),求直线
(0,c),(c为半焦距),求直线 的斜率
的斜率 的值;
的值;
(Ⅲ)试问: 的面积是否为定值?如果是,请给予证明;如果不是,请说明理由.
的面积是否为定值?如果是,请给予证明;如果不是,请说明理由.
(本小题满分13分)已知点 在椭圆
在椭圆 上,椭圆
上,椭圆 的左焦点为(-1,0)
的左焦点为(-1,0)
(1)求椭圆 的方程;
的方程;
(2)直线 过点
过点 交椭圆C于M、N两点,AB是椭圆
交椭圆C于M、N两点,AB是椭圆 经过原点
经过原点 的弦,且MN//AB,问是否存在正数
的弦,且MN//AB,问是否存在正数 ,使
,使 为定值?若存在,求出
为定值?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(本小题满分16分) 对于项数为 的有穷数列
的有穷数列 ,记
,记 ,即
,即 为
为 中的最大值,则称
中的最大值,则称 是
是 的“控制数列”,
的“控制数列”, 各项中不同数值的个数称为
各项中不同数值的个数称为 的“控制阶数”.
的“控制阶数”.
(Ⅰ)若各项均为正整数的数列 的控制数列
的控制数列 为
为 ,写出所有的
,写出所有的 ;
;
(Ⅱ)若 ,
, ,其中
,其中 ,
, 是
是 的控制数列,试用
的控制数列,试用 表示
表示 的值;
的值;
(Ⅲ)在 的所有全排列中,将每种排列视为一个数列,对于其中控制阶数为2的所有数列,求它们的首项之和.
的所有全排列中,将每种排列视为一个数列,对于其中控制阶数为2的所有数列,求它们的首项之和.
(本小题满分12分)设椭圆 的左右焦点分别为
的左右焦点分别为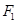 、
、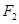 ,
,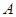 是椭圆
是椭圆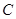 上的一点,
上的一点,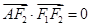 ,坐标原点
,坐标原点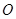 到直线
到直线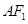 的距离为
的距离为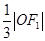 .
.
(1)求椭圆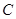 的方程;
的方程;
(2)设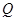 是椭圆
是椭圆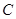 上的一点,
上的一点,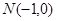 ,连接QN的直线交
,连接QN的直线交 轴于点
轴于点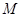 ,若
,若 ,求直线
,求直线 的斜率.
的斜率.
设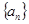 是等比数列,公比
是等比数列,公比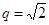 ,
,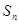 为
为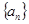 的前n项和。记
的前n项和。记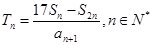 ,设
,设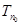 为数列
为数列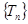 的最大项,则
的最大项,则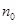 =( )
=( )
| A.3 | B.4 | C.5 | D.6 |