已知函数 在
在 处的切线
处的切线 与直线
与直线 平行.
平行.
(1)求实数 的值;
的值;
(2)若关于 的方程
的方程 在
在 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数 的取值范围;
的取值范围;
(3)记函数 ,设
,设 是函数
是函数 的两个极值点,若
的两个极值点,若 ,且
,且 恒成立,求实数
恒成立,求实数 的最大值.
的最大值.
已知椭圆C的中心在原点,左焦点为 ,右准线方程为:
,右准线方程为: .
.
(1)求椭圆C的标准方程;
(2)若椭圆C上点 到定点
到定点 的距离的最小值为1,求
的距离的最小值为1,求 的值及点
的值及点 的坐标;
的坐标;
(3)分别过椭圆C的四个顶点作坐标轴的垂线,围成如图所示的矩形,A、B是所围成的矩形在 轴上方的两个顶点.若P、Q是椭圆C上两个动点,直线OP、OQ与椭圆的另一交点分别为
轴上方的两个顶点.若P、Q是椭圆C上两个动点,直线OP、OQ与椭圆的另一交点分别为 、
、 ,且直线OP、OQ的斜率之积等于直线OA、OB的斜率之积,试探求四边形
,且直线OP、OQ的斜率之积等于直线OA、OB的斜率之积,试探求四边形 的面积是否为定值,并说明理由.
的面积是否为定值,并说明理由.
如图,在半径为 的半圆形(O为圆心)铁皮上截取一块矩形材料ABCD,其中点A、B在直径上,点C、D在圆周上,将所截得的矩形铁皮ABCD卷成一个以AD为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),记圆柱形罐子的体积为
的半圆形(O为圆心)铁皮上截取一块矩形材料ABCD,其中点A、B在直径上,点C、D在圆周上,将所截得的矩形铁皮ABCD卷成一个以AD为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),记圆柱形罐子的体积为
 .
.
(1)按下列要求建立函数关系式:
①设 ,将
,将 表示为
表示为 的函数;
的函数;
②设 (
( ),将
),将 表示为
表示为 的函数;
的函数;
(2)请您选用(1)问中的一个函数关系,求圆柱形罐子的最大体积.
已知椭圆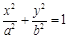
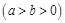 的右焦点为
的右焦点为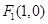 ,离心率为
,离心率为 .设A,B为椭圆上关于原点对称的两点,
.设A,B为椭圆上关于原点对称的两点,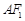 的中点为M,
的中点为M,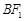 的中点为N,原点
的中点为N,原点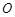 在以线段
在以线段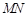 为直径的圆上.设直线AB的斜率为k,若
为直径的圆上.设直线AB的斜率为k,若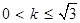 ,则
,则 的取值范围为
的取值范围为 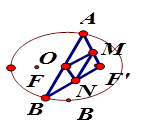
已知椭圆 经过点
经过点 ,离心率为
,离心率为 ,动点M(2,t)(
,动点M(2,t)( ).
).
(1)求椭圆的标准方程;
(2)求以OM为直径且截直线 所得的弦长为2的圆的方程;
所得的弦长为2的圆的方程;
(3)设F是椭圆的右焦点,过点F作OM的垂线与以OM为直径的圆交于点N,证明线段ON的长为定值,并求出这个定值.
(本小题满分13分)已知椭圆的焦点在 轴上,它的一个顶点恰好是抛物线
轴上,它的一个顶点恰好是抛物线 的焦点,离心率
的焦点,离心率 .
.
(1)求椭圆的标准方程;
(2)过椭圆的右焦点 作与坐标轴不垂直的直线
作与坐标轴不垂直的直线 ,交椭圆于
,交椭圆于 、
、 两点,设点
两点,设点 是线段
是线段 上的一个动点,且
上的一个动点,且 ,求
,求 的取值范围;
的取值范围;
(3)设点 是点
是点 关于
关于 轴的对称点,在
轴的对称点,在 轴上是否存在一个定点
轴上是否存在一个定点 ,使得
,使得 、
、 、
、 三点共线?若存在,求出定点
三点共线?若存在,求出定点 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
本题共有3个小题,第一小题3分,第二小题7分,第三小题6分
如图,曲线 由曲线
由曲线 和曲线
和曲线 组成,其中点
组成,其中点 为曲线
为曲线 所在圆锥曲线的焦点,点
所在圆锥曲线的焦点,点 为曲线
为曲线 所在圆锥曲线的焦点,
所在圆锥曲线的焦点,
(1)若 ,求曲线
,求曲线 的方程;
的方程;
(2)如图,作直线 平行于曲线
平行于曲线 的渐近线,交曲线
的渐近线,交曲线 于点A、B,求证:弦AB的中点M必在曲线
于点A、B,求证:弦AB的中点M必在曲线 的另一条渐近线上;
的另一条渐近线上;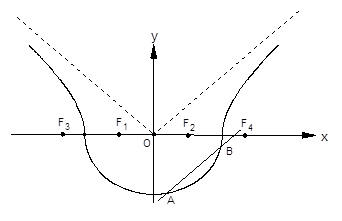
(3)对于(1)中的曲线 ,若直线
,若直线 过点
过点 交曲线
交曲线 于点C、D,求
于点C、D,求 面积的最大值。
面积的最大值。
已知函数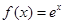 ,
,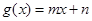 .
.
(1)设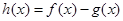 .
.
① 若函数 在
在 处的切线过点
处的切线过点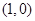 ,求
,求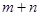 的值;
的值;
② 当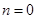 时,若函数
时,若函数 在
在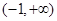 上没有零点,求
上没有零点,求 的取值范围;
的取值范围;
(2)设函数 ,且
,且 ,求证:当
,求证:当 时,
时, .
.
设数列 是各项均为正数的等比数列,其前
是各项均为正数的等比数列,其前 项和为
项和为 ,若
,若 ,
, .
.
(1)求数列 的通项公式;
的通项公式;
(2)对于正整数 (
( ),求证:“
),求证:“ 且
且 ”是“
”是“ 这三项经适当排序后能构成等差数列”成立的充要条件;
这三项经适当排序后能构成等差数列”成立的充要条件;
(3)设数列 满足:对任意的正整数
满足:对任意的正整数 ,都有
,都有
 ,且集合
,且集合 中有且仅有3个元素,试求
中有且仅有3个元素,试求 的取值范围.
的取值范围.
在平面直角坐标系 中,椭圆
中,椭圆 的右准线方程为
的右准线方程为 ,右顶点为
,右顶点为 ,
,
上顶点为 ,右焦点为
,右焦点为 ,斜率为
,斜率为 的直线
的直线 经过点
经过点 ,且点
,且点 到直线
到直线 的距离为
的距离为 .
.
(1)求椭圆 的标准方程;
的标准方程;
(2)将直线 绕点
绕点 旋转,它与椭圆
旋转,它与椭圆 相交于另一点
相交于另一点 ,当
,当 三点共线时,试确定直线
三点共线时,试确定直线 的斜率.
的斜率.
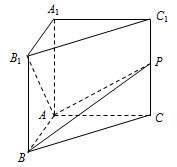
如图,在直三棱柱 中,
中, ,
,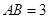 ,
, ,动点
,动点 满足
满足 ,当
,当 时,
时,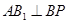 .
.
(1)求棱 的长;
的长;
(2)若二面角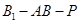 的大小为
的大小为 ,求
,求 的值..
的值..
在平面直角坐标系 中,椭圆
中,椭圆 的右准线方程为
的右准线方程为 ,右顶点为
,右顶点为 ,
,
上顶点为 ,右焦点为
,右焦点为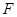 ,斜率为
,斜率为 的直线
的直线 经过点
经过点 ,且点
,且点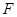 到直线
到直线 的距离为
的距离为 .
.
(1)求椭圆 的标准方程;
的标准方程;
(2)将直线 绕点
绕点 旋转,它与椭圆
旋转,它与椭圆 相交于另一点
相交于另一点 ,当
,当 三点共线时,试确定直线
三点共线时,试确定直线 的斜率.
的斜率.
(本小题满分14分)已知函数 (
( 是常数).
是常数).
(1)设 ,
, 、
、 是函数
是函数 的极值点,试证明曲线
的极值点,试证明曲线 关于点
关于点 对称;
对称;
(2)是否存在常数 ,使得
,使得 ,
, 恒成立?若存在,求常数
恒成立?若存在,求常数 的值或取值范围;若不存在,请说明理由.
的值或取值范围;若不存在,请说明理由.
(注:,对于曲线 上任意一点
上任意一点 ,若点
,若点 关于
关于 的对称点为
的对称点为 ,则
,则 在曲线
在曲线 上.)
上.)
(本小题满分13分)设椭圆 (a>b>0)的离心率e=
(a>b>0)的离心率e= ,左顶点M到直线
,左顶点M到直线 的距离d=
的距离d= ,O为坐标原点.
,O为坐标原点.
(1)求椭圆C的方程;
(2)设直线l与椭圆C交于A、B两点,若以AB为直径的圆经过坐标原点,证明:点O到直线AB的距离为定值;
(3)在(2)的条件下,试求△AOB的面积S的最小值.