在直角坐标系 ,椭圆
,椭圆 的左、右焦点分别为
的左、右焦点分别为 .其中
.其中 也是抛物线
也是抛物线 的焦点,点M为
的焦点,点M为 在第一象限的交点,且
在第一象限的交点,且 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)若过点D(4,0)的直线 交于不同的两点A、B,且A在DB之间,试求
交于不同的两点A、B,且A在DB之间,试求 BOD面积之比的取值范围.
BOD面积之比的取值范围.
设抛物线C1:y2=4x的准线与x轴交于点F1,焦点为F2;以F1,F2为焦点,离心率为 的椭圆记作C2
的椭圆记作C2
(1)求椭圆的标准方程;
(2)直线L经过椭圆C2的右焦点F2,与抛物线C1交于A1,A2两点,与椭圆C2交于B1,B2两点。当以B1B2为直径的圆经过F1时,求|A1A2|长。
(3)若M是椭圆上的动点,以M为圆心,MF2为半径作圆 ,是否存在定圆
,是否存在定圆 ,使得
,使得 与
与 恒相切?若存在,求出
恒相切?若存在,求出 的方程,若不存在,请说明理由。
的方程,若不存在,请说明理由。
(本小题满分12分)已知函数 (a是实数),
(a是实数), +1。
+1。
(1)若函数f(x)在[1,+ )上是单调函数,求a的取值范围;
)上是单调函数,求a的取值范围;
(2)是否存在正实数a满足:对于任意 ,总存在
,总存在 ,使得f(x1)=g(x2)成立,若存在求出a的范围,若不存在,说明理由。
,使得f(x1)=g(x2)成立,若存在求出a的范围,若不存在,说明理由。
(3)若数列 满足
满足 ,求证:
,求证: 。
。
(本小题满分12分)设抛物线C1:y2=4x的准线与x轴交于点F1,焦点为F2;以F1,F2为焦点,离心率为 的椭圆记作C2
的椭圆记作C2
(1)求椭圆的标准方程;
(2)直线L经过椭圆C2的右焦点F2,与抛物线C1交于A1,A2两点,与椭圆C2交于B1,B2两点。当以B1B2为直径的圆经过F1时,求|A1A2|长。
(3)若M是椭圆上的动点,以M为圆心,MF2为半径作圆 ,是否存在定圆
,是否存在定圆 ,使得
,使得 与
与 恒相切?若存在,求出
恒相切?若存在,求出 的方程,若不存在,请说明理由。
的方程,若不存在,请说明理由。
(本小题满分12分)如图,在四棱台ABCD-A1B1C1D1中,DD1 平面ABCD,底面ABCD是平行四边形,AB=AD=2A1B1,
平面ABCD,底面ABCD是平行四边形,AB=AD=2A1B1,

(1)证明:BB1 AC;
AC;
(2)若AB=2,且二面角A1-AB-C大小为60 ,连接AC,BD,设交点为O,连接B1O。求三棱锥B1-ABO外接球的体积。(球体体积公式:
,连接AC,BD,设交点为O,连接B1O。求三棱锥B1-ABO外接球的体积。(球体体积公式: ,R是球半径)
,R是球半径)
若椭圆 的方程为
的方程为 ,
, 、
、 是它的左、右焦点,椭圆
是它的左、右焦点,椭圆 过点
过点 ,且离心率为
,且离心率为 .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)设椭圆的左右顶点为 、
、 ,直线
,直线 的方程为
的方程为 ,
, 是椭圆上任一点,直线
是椭圆上任一点,直线 、
、 分别交直线
分别交直线 于
于 、
、 两点,求
两点,求 的值;
的值;
(Ⅲ)过点 任意作直线
任意作直线 (与
(与 轴不垂直)与椭圆
轴不垂直)与椭圆 交于
交于 、
、 两点,与
两点,与 轴交于
轴交于 点
点 ,
, .证明:
.证明: 为定值.
为定值.
(本小题满分13分)若存在实常数 和
和 ,使得函数
,使得函数 和
和 对其定义域上的任意实数
对其定义域上的任意实数 分别满足:
分别满足: 和
和 ,则称直线
,则称直线 为
为 和
和 的“隔离直线”.已知
的“隔离直线”.已知 ,
, 为自然对数的底数).
为自然对数的底数).
(1)求 的极值;
的极值;
(2)函数 和
和 是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.
是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.
(本小题满分13分)已知 为正实数,
为正实数, 为自然数,抛物线
为自然数,抛物线 与
与 轴正半轴相交于点
轴正半轴相交于点 ,设
,设 为该抛物线在点
为该抛物线在点 处的切线在
处的切线在 轴上的截距.
轴上的截距.
(1)用 和
和 表示
表示 ;
;
(2)求对所有 都有
都有 成立的
成立的 的最小值;
的最小值;
(3)当 时,比较
时,比较 与
与 的大小,并说明理由.
的大小,并说明理由.
某旅游景区的观景台P位于高为 的山峰上(即山顶到山脚水平面M的垂直高度
的山峰上(即山顶到山脚水平面M的垂直高度 ),山脚下有一段位于水平线上笔直的公路AB,山坡面可近似地看作平面PAB,且
),山脚下有一段位于水平线上笔直的公路AB,山坡面可近似地看作平面PAB,且 为以
为以 为底边的等腰三角形.山坡面与山脚所在水平面M所成的二面角为
为底边的等腰三角形.山坡面与山脚所在水平面M所成的二面角为 ,且
,且 .现从山脚的水平公路AB某处C0开始修建一条盘山公路,该公路的第一段,第二段,第三段,…,第n-1段依次为C0C1,C1C2,C2C3,…,Cn-1Cn(如图所示),C0C1,C1C2,C2C3,…,Cn-1Cn与AB所成的角均为
.现从山脚的水平公路AB某处C0开始修建一条盘山公路,该公路的第一段,第二段,第三段,…,第n-1段依次为C0C1,C1C2,C2C3,…,Cn-1Cn(如图所示),C0C1,C1C2,C2C3,…,Cn-1Cn与AB所成的角均为 ,且
,且 .
.
(1)问每修建盘山公路多少米,垂直高度就能升高100米? 若修建盘山公路至半山腰(高度为山高的一半),在半山腰的中心Q处修建上山缆车索道站,索道PQ依山而建(与山坡面平行,离坡面高度忽略不计),问盘山公路的长度和索道的长度各是多少 ?
?
(2)若修建 盘山公路,其造价为
盘山公路,其造价为 万元.修建索道的造价为
万元.修建索道的造价为 万元
万元 .问修建盘山公路至多高时,再修建上山索道至观景台,总造价最少?
.问修建盘山公路至多高时,再修建上山索道至观景台,总造价最少?
如图, 的外接圆
的外接圆 的半径为
的半径为 ,
, 所在的平面,
所在的平面, ,
, ,
, ,且
,且 ,
, .
.
(1)求证:平面ADC 平面BCDE.
平面BCDE.
(2)试问线段DE上是否存在点M,使得直线AM与平面ACD所成角的正弦值为 ?若存在,
?若存在,
确定点M的位置,若不存在,请说明理由.
衡阳市八中对参加“社会实践活动”的全体志愿者进行学分考核,因该批志愿者表现良好,学校决定考核只有合格和优秀两个等次.若某志愿者考核为合格,授予1个学分;考核为优秀,授予2个学分,假设该校志愿者甲、乙、丙考核为优秀的概率分别为 、
、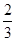 、
、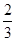 ,他们考核所得的等次相互独立.
,他们考核所得的等次相互独立.
(1)求在这次考核中,志愿者甲、乙、丙三人中至少有一名考核为优秀的概率;
(2)记在这次考核中甲、乙、丙三名志愿者所得学分之和为随机变量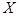 ,求随机变量
,求随机变量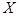 的分布列及数学期望.
的分布列及数学期望.
(本小题满分12分)已知函数 (
( 为常数)的图像与
为常数)的图像与 轴交于点
轴交于点 ,曲线
,曲线 在点
在点 处的切线斜率为-1.
处的切线斜率为-1.
(1)求 的值及函数
的值及函数 的极值; (2)证明:当
的极值; (2)证明:当 时,
时, 。
。
(本小题满分12分)如图所示,在平面直角坐标系 中,设椭圆
中,设椭圆 ,其中
,其中 ,过椭圆
,过椭圆 内一点
内一点
 的两条直线分别与椭圆交于点
的两条直线分别与椭圆交于点 和
和 ,且满足
,且满足 ,
, ,其中
,其中 为正常数. 当点
为正常数. 当点 恰为椭圆的右顶点时,对应的
恰为椭圆的右顶点时,对应的 .
.
(1)求椭圆 的离心率;
的离心率;
(2)求 与
与 的值;
的值;
(3)当 变化时,
变化时, 是否为定值?若是,请求出此定值;若不是,请说明理由.
是否为定值?若是,请求出此定值;若不是,请说明理由.
抛物线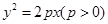 的焦点为
的焦点为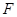 ,准线为
,准线为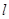 ,
,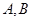 是抛物线上的两个动点,且满足
是抛物线上的两个动点,且满足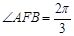 .设线段
.设线段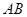 的中点
的中点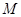 在
在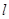 上的投影为
上的投影为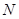 ,则
,则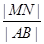 的最大值是
的最大值是
A.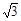 |
B.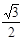 |
C.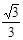 |
D.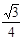 |