(本小题满分12分)如图所示,在平面直角坐标系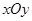 中,设椭圆
中,设椭圆 ,其中
,其中 ,过椭圆
,过椭圆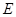 内一点
内一点
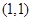 的两条直线分别与椭圆交于点
的两条直线分别与椭圆交于点 和
和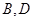 ,且满足
,且满足 ,
, ,其中
,其中 为正常数. 当点
为正常数. 当点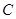 恰为椭圆的右顶点时,对应的
恰为椭圆的右顶点时,对应的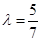 .
.
(1)求椭圆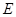 的离心率;
的离心率;
(2)求 与
与 的值;
的值;
(3)当 变化时,
变化时,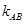 是否为定值?若是,请求出此定值;若不是,请说明理由.
是否为定值?若是,请求出此定值;若不是,请说明理由.
推荐套卷
(本小题满分12分)如图所示,在平面直角坐标系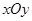 中,设椭圆
中,设椭圆 ,其中
,其中 ,过椭圆
,过椭圆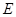 内一点
内一点
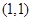 的两条直线分别与椭圆交于点
的两条直线分别与椭圆交于点 和
和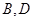 ,且满足
,且满足 ,
, ,其中
,其中 为正常数. 当点
为正常数. 当点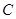 恰为椭圆的右顶点时,对应的
恰为椭圆的右顶点时,对应的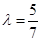 .
.
(1)求椭圆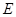 的离心率;
的离心率;
(2)求 与
与 的值;
的值;
(3)当 变化时,
变化时,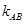 是否为定值?若是,请求出此定值;若不是,请说明理由.
是否为定值?若是,请求出此定值;若不是,请说明理由.