湖北省武汉市武昌区高三元月调研考试理科数学试卷
已知 ,
, ,“存在点
,“存在点 ”是“
”是“ ”的
”的
| A.充分而不必要的条件 | B.必要而不充分的条件 |
| C.充要条件 | D.既不充分也不必要的条件 |
根据如下样本数据
| x |
3 |
4 |
5 |
6 |
7 |
| y |
4.0 |
2.5 |
 0.5 0.5 |
0.5 |
 2.0 2.0 |
得到的回归方程为 .若
.若 ,则
,则 每增加1个单位,
每增加1个单位, 就
就
A.增加 个单位 B.减少
个单位 B.减少 个单位
个单位
C.增加 个单位 D.减少
个单位 D.减少 个单位
个单位
如图,取一个底面半径和高都为R的圆柱,从圆柱中挖去一个以圆柱的上底面为底面,下底面圆心为顶点的圆锥,把所得的几何体与一个半径为R的半球放在同一水平面 上.用一平行于平面
上.用一平行于平面 的平面去截这两个几何体,截面分别为圆面和圆环面(图中阴影部分).设截面面积分别为
的平面去截这两个几何体,截面分别为圆面和圆环面(图中阴影部分).设截面面积分别为 和
和 ,那么
,那么
A.   |
B. = = |
C.   |
D.不确定 |
一个几何体的三视图如图所示,则该几何体的表面积和体积分别是
A.24+ 和40 和40 |
B.24+ 和72 和72 |
C.64+ 和40 和40 |
D.50+ 和72 和72 |
已知x,y满足约束条件 若z=y-ax取得最大值的最优解不唯一,则实数a的值为
若z=y-ax取得最大值的最优解不唯一,则实数a的值为
A. 或-1 或-1 |
B.2或 |
C.2或1 | D.2或-1 |
如图,矩形ABCD的四个顶点的坐标分别为A(0,—1),B( ,—1),C(
,—1),C( ,1),D(0,1),正弦曲线f(x)=sinx和余弦曲线g(x)=cosx在矩形ABCD内交于点F,向矩形ABCD区域内随机投掷一点,则该点落在阴影区域内的概率是
,1),D(0,1),正弦曲线f(x)=sinx和余弦曲线g(x)=cosx在矩形ABCD内交于点F,向矩形ABCD区域内随机投掷一点,则该点落在阴影区域内的概率是
A. |
B. |
C. |
D. |
抛物线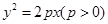 的焦点为
的焦点为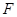 ,准线为
,准线为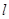 ,
,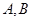 是抛物线上的两个动点,且满足
是抛物线上的两个动点,且满足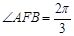 .设线段
.设线段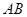 的中点
的中点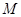 在
在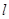 上的投影为
上的投影为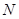 ,则
,则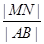 的最大值是
的最大值是
A.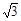 |
B.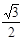 |
C.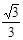 |
D.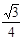 |
已知函数 是定义在R上的奇函数,它的图象关于直线
是定义在R上的奇函数,它的图象关于直线 对称,且
对称,且
 .若函数
.若函数 在区间
在区间 上有10个零点(互不相同),则实数
上有10个零点(互不相同),则实数 的取值范围是
的取值范围是
A. |
B. |
C. |
D. |
设斜率为 的直线
的直线 与双曲线
与双曲线 交于不同的两点P、Q,若点P、Q在
交于不同的两点P、Q,若点P、Q在 轴上的射影恰好为双曲线的两个焦点,则该双曲线的离心率是 .
轴上的射影恰好为双曲线的两个焦点,则该双曲线的离心率是 .
“渐升数”是指除最高位数字外,其余每一个数字比其左边的数字大的正整数(如13456和35678都是五位的“渐升数”).
(Ⅰ)共有 个五位“渐升数”(用数字作答);
(Ⅱ)如果把所有的五位“渐升数”按照从小到大的顺序排列,则第110个五位“渐升数”是 .
过圆外一点P作圆的切线PA(A为切点),再作割线PBC依次交圆于B,C.若PA=6,AC=8,BC=9,则AB=________.
已知曲线 的参数方程是
的参数方程是 (
( 为参数,a为实数常数),曲线
为参数,a为实数常数),曲线 的参数方程是
的参数方程是 (
( 为参数,b为实数常数).以坐标原点为极点,
为参数,b为实数常数).以坐标原点为极点, 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线 的极坐标方程是
的极坐标方程是 . 若
. 若 与
与 分曲线
分曲线 所成长度相等的四段弧,则
所成长度相等的四段弧,则 .
.
(本小题满分11分)已知函数 的在区间
的在区间 上的最小值为0.
上的最小值为0.
(Ⅰ)求常数a的值;
(Ⅱ)当 时,求使
时,求使 成立的x的集合.
成立的x的集合.
(本小题满分12分)已知等差数列{an}的首项为1,前n项和为 ,且S1,S2,S4成等比数列.
,且S1,S2,S4成等比数列.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)记 为数列
为数列 的前
的前 项和,是否存在正整数n,使得
项和,是否存在正整数n,使得 ?若存在,求
?若存在,求 的最大值;若不存在,说明理由.
的最大值;若不存在,说明理由.
(本小题满分12分)如图,在棱长为2的正方体 中,点E,F分别是棱AB,BC上的动点,且AE=BF.
中,点E,F分别是棱AB,BC上的动点,且AE=BF.
(Ⅰ)求证:A1F C1E;
C1E;
(Ⅱ)当三棱锥 的体积取得最大值时,求二面角
的体积取得最大值时,求二面角 的正切值.
的正切值.
(本小题满分12分)对某交通要道以往的日车流量(单位:万辆)进行统计,得到如下记录:
| 日车流量x |
 |
 |
 |
 |
 |
 |
| 频率 |
0.05 |
0.25 |
0.35 |
0.25 |
0.10 |
0 |
将日车流量落入各组的频率视为概率,并假设每天的车流量相互独立.
(Ⅰ)求在未来连续3天里,有连续2天的日车流量都不低于10万辆且另1天的日车流量低于5万辆的概率;
(Ⅱ)用X表示在未来3天时间里日车流量不低于10万辆的天数,求X的分布列和数学期望.
(本小题满分14分)已知椭圆C: 的焦距为4,其长轴长和短轴长之比为
的焦距为4,其长轴长和短轴长之比为 .
.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)设F为椭圆C的右焦点,T为直线 上纵坐标不为0的任意一点,过F作TF的垂线交椭圆C于点P,Q.
上纵坐标不为0的任意一点,过F作TF的垂线交椭圆C于点P,Q.
(ⅰ)若OT平分线段PQ(其中O为坐标原点),求 的值;
的值;
(ⅱ)在(ⅰ)的条件下,当 最小时,求点T的坐标.
最小时,求点T的坐标.
 ,则
,则


 的展开式中x3项的系数为20,则a2 +b2的最小值为
的展开式中x3项的系数为20,则a2 +b2的最小值为 的边长为
的边长为 ,
, 为
为 的中点,
的中点,  为
为 的中点,则
的中点,则 _______.
_______. 的通项公式是_______.
的通项公式是_______.
 (a为常数),曲线y=f(x)在与y轴的交点A处的切线斜率为-1.
(a为常数),曲线y=f(x)在与y轴的交点A处的切线斜率为-1. 时,
时, ;
; 时,
时, .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号