(本小题满分14分)已知数列 满足
满足 ,
, ,
, .
.
(1)求证:数列 是等差数列;
是等差数列;
(2)求证: .
.
(本小题满分14分)已知椭圆
 (
( )的长轴长为
)的长轴长为 ,且过点
,且过点 .
.
(1)求椭圆 的方程;
的方程;
(2)设 、
、 、
、 是椭圆上的三点,若
是椭圆上的三点,若 ,点
,点 为线段
为线段 的中点,
的中点, 、
、 两点的坐标分别为
两点的坐标分别为 、
、 ,求证:
,求证: .
.
(本小题满分14分)设函数 .
.
(1)当 时,求
时,求 的极值;
的极值;
(2)设A、B是曲线 上的两个不同点,且曲线在A、B两点处的切线均与
上的两个不同点,且曲线在A、B两点处的切线均与 轴平行,直线AB的斜率为
轴平行,直线AB的斜率为 ,是否存在
,是否存在 ,使得
,使得 若存在,请求出
若存在,请求出 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
(本小题满分12分)已知A(-2,0),B(2,0)为椭圆C的左、右顶点,F为其右焦点,P是椭圆C上异于A,B的动点,△APB面积的最大值为2 .
.
(1)求椭圆C的标准方程;
(2)若直线AP的倾斜角为 ,且与椭圆在点B处的切线交于点D,试判断以BD为直径的圆与直线PF的位置关系,并加以证明.
,且与椭圆在点B处的切线交于点D,试判断以BD为直径的圆与直线PF的位置关系,并加以证明.
(本小题满分13分)已知数列 满足
满足 ,
, ,数列
,数列 的前n项和为
的前n项和为 ,
, ,其中
,其中 .
.
(1)求 的值;
的值;
(2)证明:数列 为等比数列;
为等比数列;
(3)是否存在 ,使得
,使得 若存在,求出所有的n的值;若不存在,请说明理由.
若存在,求出所有的n的值;若不存在,请说明理由.
某工厂生产一种产品的原材料费为每件40元,若用 表示该厂生产这种产品的总件数,则电
表示该厂生产这种产品的总件数,则电
力与机器保养等费用为每件 元,又该厂职工工资固定支出12500元。
元,又该厂职工工资固定支出12500元。
(1)把每件产品的成本费 (元)表示成产品件数
(元)表示成产品件数 的函数,并求每件产品的最低成本费;
的函数,并求每件产品的最低成本费;
(2)如果该厂生产的这种产品的数量 不超过3000件,且产品能全部销售,根据市场调查:每件产品的
不超过3000件,且产品能全部销售,根据市场调查:每件产品的
销售价 与产品件数
与产品件数 有如下关系:
有如下关系: ,试问生产多少件产品,总利润最高?总利润
,试问生产多少件产品,总利润最高?总利润
最高为多少?(总利润 总销售额
总销售额 总成本)
总成本)
一座拱桥桥洞的截面边界由抛物线弧段 和矩形
和矩形 的三边组成,拱的顶部
的三边组成,拱的顶部 距离水面
距离水面 ,水面上的矩形的高度为
,水面上的矩形的高度为 ,水面宽
,水面宽 ,如图所示.一艘船运载一个长方体形的集装箱,此箱平放在船上.已知船宽
,如图所示.一艘船运载一个长方体形的集装箱,此箱平放在船上.已知船宽 ,船面距离水面
,船面距离水面 ,集装箱的尺寸为长×宽×高=
,集装箱的尺寸为长×宽×高= .试问此船能否通过此桥?并说明理由.
.试问此船能否通过此桥?并说明理由.
设动点
 到定点
到定点 的距离比到
的距离比到 轴的距离大
轴的距离大 .记点
.记点 的轨迹为曲线
的轨迹为曲线 .
.
(1)求点 的轨迹方程;
的轨迹方程;
(2)设圆 过
过 ,且圆心
,且圆心 在
在 的轨迹上,
的轨迹上, 是圆
是圆 在
在 轴上截得的弦,当
轴上截得的弦,当 运动时弦长
运动时弦长 是否为定值?说明理由;
是否为定值?说明理由;
(3)过 做互相垂直的两直线交曲线
做互相垂直的两直线交曲线 于
于 ,求四边形
,求四边形 面积的最小值.
面积的最小值.
如图放置的边长为1的正方形PABC沿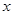 轴滚动。设顶点P(
轴滚动。设顶点P(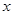 ,y)的轨迹方程是
,y)的轨迹方程是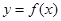 ,则
,则 的最小正周期为 ;
的最小正周期为 ;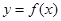 在其两个相邻零点间的图像与
在其两个相邻零点间的图像与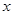 轴所围区域的面积为 。
轴所围区域的面积为 。 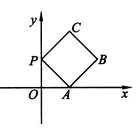
说明:“正方形PABC沿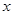 轴滚动”包括沿
轴滚动”包括沿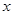 轴正方向和沿
轴正方向和沿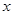 轴负方向滚动。沿
轴负方向滚动。沿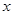 轴正方向滚动指的是先以顶点A为中心顺时针旋转,当顶点B落在
轴正方向滚动指的是先以顶点A为中心顺时针旋转,当顶点B落在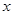 轴上时,再以顶点B为中心顺时针旋转,如此继续。类似地,正方形PABC可以沿
轴上时,再以顶点B为中心顺时针旋转,如此继续。类似地,正方形PABC可以沿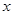 轴负方向滚动。
轴负方向滚动。
(本小题共13分)已知数列 的前
的前 项和
项和 满足
满足 ,
, ,
, .
.
(Ⅰ)如果 ,求数列
,求数列 的通项公式;
的通项公式;
(Ⅱ)如果 ,求证:数列
,求证:数列 为等比数列,并求
为等比数列,并求 ;
;
(Ⅲ)如果数列 为递增数列,求
为递增数列,求 的取值范围.
的取值范围.
(本小题满分13分)设集合 由满足下列两个条件的数列
由满足下列两个条件的数列 构成:
构成:
① ②存在实数
②存在实数 ,使
,使 .(
.( 为正整数)
为正整数)
(Ⅰ)在只有 项的有限数列
项的有限数列 ,
, 中,其中
中,其中 ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,试判断数列
,试判断数列 ,
, 是否为集合
是否为集合 的元素;
的元素;
(Ⅱ)设 是等差数列,
是等差数列, 是其前
是其前 项和,
项和, ,
, ,证明数列
,证明数列 ;并求出
;并求出 的取值范围.
的取值范围.