北京市丰台区高三上学期期末考试文科数学试卷
在复平面内,复数 对应的点的坐标是
对应的点的坐标是
| A.(-1,1) | B.(-1, -1) | C.(1, -1) | D.(1,1) |
等差数列{an}的前n项和为Sn,如果a1=2,a3+ a5=22,那么S3等于
| A.8 | B.15 | C.24 | D.30 |
已知 ,
, ,
, ,则a,b,c的大小关系是
,则a,b,c的大小关系是
| A.a > b > c | B.c > b > a | C.c > a >b | D.a>c>b |
甲、乙两名同学在5次体能测试中的成绩的茎叶图如图所示,设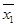 ,
,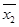 分别表示甲、乙两名同学测试成绩的平均数,
分别表示甲、乙两名同学测试成绩的平均数,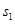 ,
,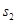 分别表示甲、乙两名同学测试成绩的标准差,则有
分别表示甲、乙两名同学测试成绩的标准差,则有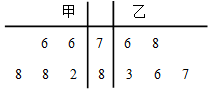
A.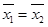 , ,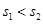 |
B.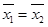 , ,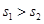 |
C.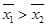 , ,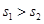 |
D.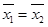 , ,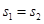 |
在平面直角坐标系xOy中,如果菱形OABC的边长为2,点A在x轴上,则菱形内(不含边界)整点(横纵坐标都是整数的点)个数的取值集合是
| A.{1,2} | B.{1,2,3} | C.{0,1,2} | D.{0,1,2,3} |
已知圆C: ,那么圆心坐标是 ;如果圆C的弦AB的中点坐标是(-2,3),那么弦AB所在的直线方程是___.
,那么圆心坐标是 ;如果圆C的弦AB的中点坐标是(-2,3),那么弦AB所在的直线方程是___.
设函数 与
与 是定义在同一区间
是定义在同一区间 上的两个函数,如果函数
上的两个函数,如果函数 在区间
在区间 上有
上有 个不同的零点,那么称函数
个不同的零点,那么称函数 和
和 在区间
在区间 上为“
上为“ 阶关联函数”.现有如下三组函数:
阶关联函数”.现有如下三组函数:
① ,
, ;
;
② ,
, ; ③
; ③ ,
, .
.
其中在区间 上是“
上是“ 阶关联函数”的函数组的序号是___.(写出所有满足条件的函数组的序号)
阶关联函数”的函数组的序号是___.(写出所有满足条件的函数组的序号)
(本小题共13分)已知函数 ,
, .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)求函数 在区间
在区间 上的最大值和最小值,及相应的x的值.
上的最大值和最小值,及相应的x的值.
(本小题共13分)某市为了了解本市高中学生的汉字书写水平,在全市范围内随机抽取了近千名学生参加汉字听写考试,将所得数据进行分组,分组区间为:[50,60),[60,70),[70,80),[80,90),[90,100],并绘制出频率分布直方图,如图所示.
(Ⅰ)求频率分布直方图中的a值;从该市随机选取一名学生,试估计这名学生参加考试的成绩低于90分的概率;
(Ⅱ)设A,B,C三名学生的考试成绩在区间[80,90)内,M,N两名学生的考试成绩在区间[60,70)内,现从这5名学生中任选两人参加座谈会,求学生M,N至少有一人被选中的概率;
(Ⅲ)试估计样本的中位数落在哪个分组区间内 (只需写出结论).
(注:将频率视为相应的概率)
(本小题共14分)如图,在四棱锥S-ABCD中,底面ABCD为菱形,∠BAD=60°,平面SAD⊥平面ABCD,SA=SD,E,P,Q分别是棱AD,SC,AB的中点.
(Ⅰ)求证:PQ∥平面SAD;
(Ⅱ)求证:AC⊥平面SEQ;
(Ⅲ)如果SA=AB=2,求三棱锥S-ABC的体积.
(本小题共14分)在平面直角坐标系 中,椭圆
中,椭圆 :
: 的一个顶点为
的一个顶点为 ,离心率为
,离心率为 .
.
(Ⅰ)求椭圆 的标准方程;
的标准方程;
(Ⅱ)直线 过点
过点 ,过
,过 作
作 的平行线交椭圆
的平行线交椭圆 于P,Q两点,如果以PQ为直径的圆与直线
于P,Q两点,如果以PQ为直径的圆与直线 相切,求
相切,求 的方程.
的方程.
 x>0,
x>0, ,则
,则 是
是
 ,
,
 ,
, ,
,
 ,
, (b>0且b≠1)的图象如图所示,那么函数
(b>0且b≠1)的图象如图所示,那么函数 的图象可能是
的图象可能是



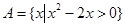 ,
,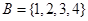 ,则
,则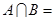 .
.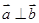 ,且
,且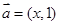 ,
,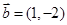 ,那么实数x= ;
,那么实数x= ; 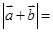 .
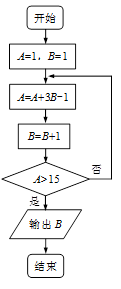
.
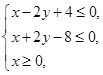 且
且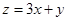 ,那么z的取值范围是___.
,那么z的取值范围是___. .
. 的极小值;
的极小值; 能否存在曲线
能否存在曲线 的切线,请说明理由.
的切线,请说明理由. 的前
的前 项和
项和 满足
满足 ,
, ,
, .
. ,求数列
,求数列 ,求证:数列
,求证:数列 为等比数列,并求
为等比数列,并求 的取值范围.
的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号