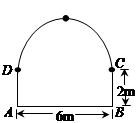一座拱桥桥洞的截面边界由抛物线弧段
和矩形
的三边组成，拱的顶部
距离水面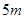
，水面上的矩形的高度为
，水面宽
，如图所示．一艘船运载一个长方体形的集装箱，此箱平放在船上．已知船宽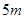，船面距离水面
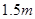，集装箱的尺寸为长×宽×高=
．试问此船能否通过此桥？并说明理由．
；
，
的面积
，求
的值
，试讨论此函数的单调性。
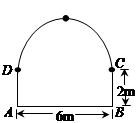
的方程．相关知识点
推荐套卷
一座拱桥桥洞的截面边界由抛物线弧段和矩形的三边组成，拱的顶部距离水面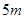，水面上的矩形的高度为，水面宽，如图所示．一艘船运载一个长方体形的集装箱，此箱平放在船上．已知船宽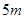，船面距离水面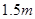，集装箱的尺寸为长×宽×高=．试问此船能否通过此桥？并说明理由．
粤公网安备 44130202000953号