如图,一简单几何体的一个面 内接于圆
内接于圆 ,
, 分别是
分别是 的中点,
的中点,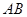 是圆
是圆 的直径,四边形
的直径,四边形 为平行四边形,且
为平行四边形,且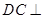 平面
平面 .
.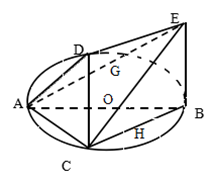
(1)求证: 平面
平面 ;
;
(2)若AC=BC=BE=2,求二面角O-CE-B的余弦值.
相关知识点
推荐套卷
如图,一简单几何体的一个面 内接于圆
内接于圆 ,
, 分别是
分别是 的中点,
的中点,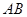 是圆
是圆 的直径,四边形
的直径,四边形 为平行四边形,且
为平行四边形,且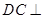 平面
平面 .
.
(1)求证: 平面
平面 ;
;
(2)若AC=BC=BE=2,求二面角O-CE-B的余弦值.