已知正项数列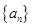 ,
,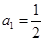 ,且
,且
(1)求证: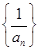 是等差数列,并求
是等差数列,并求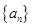 的通项公式;
的通项公式;
(2)数列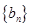 满足
满足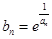 ,若
,若 ,仍是
,仍是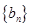 中的项,求
中的项,求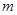 在区间
在区间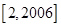 中的所有可能值之和
中的所有可能值之和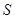 ;
;
(3)若将上述递推关系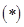 改为:
改为: ,且数列
,且数列 中任意项
中任意项 ,试求满足要求的实数
,试求满足要求的实数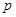 的取值范围
的取值范围
相关知识点
推荐套卷
已知正项数列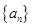 ,
,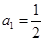 ,且
,且
(1)求证: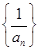 是等差数列,并求
是等差数列,并求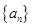 的通项公式;
的通项公式;
(2)数列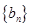 满足
满足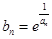 ,若
,若 ,仍是
,仍是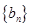 中的项,求
中的项,求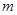 在区间
在区间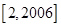 中的所有可能值之和
中的所有可能值之和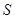 ;
;
(3)若将上述递推关系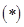 改为:
改为: ,且数列
,且数列 中任意项
中任意项 ,试求满足要求的实数
,试求满足要求的实数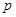 的取值范围
的取值范围