(本小题满分12分)
如图,ABCD为梯形, 平面ABCD,AB//CD,
平面ABCD,AB//CD,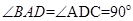
 ,E为BC中点,连结AE,交BD于O.
,E为BC中点,连结AE,交BD于O.
(I)平面 平面PAE
平面PAE
(II)求二面角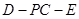 的大小(若非特殊角,求出其余弦即可)
的大小(若非特殊角,求出其余弦即可)
已知函数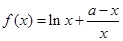 ,其中
,其中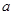 为常数,且
为常数,且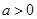 .
.
(I)若曲线 在点
在点 处的切线与直线
处的切线与直线 垂直,求
垂直,求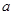 的值;
的值;
(II)若函数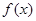 在区间
在区间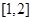 上的最小值为
上的最小值为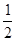 ,求
,求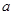 的值.
的值.
已知函数
 ,
, .
.
(1)当
 时,求函数
时,求函数 的最小值;
的最小值;
(2)若对任意  ,
, 恒成立,试求实数
恒成立,试求实数 的取值范围.
的取值范围.
选修4-4:坐标系与参数方程[(本小题满分10分)
己知直线  的参数方程为
的参数方程为 (t为参数),圆C的参数方程为
(t为参数),圆C的参数方程为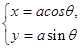 .(a>0.
.(a>0.  为参数),点P是圆C上的任意一点,若点P到直线
为参数),点P是圆C上的任意一点,若点P到直线 的距离的最大值为
的距离的最大值为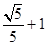 ,求a的值。
,求a的值。
(本小题满分14分)已知函数 ,过点
,过点 作曲线
作曲线 的两条切线
的两条切线 ,
, ,切点分别为
,切点分别为 ,
, .
.
(1)当 时,求函数
时,求函数 的单调递增区间;
的单调递增区间;
(2)设 ,求函数
,求函数 的表达式;
的表达式;
(3)在(2)的条件下,若对任意的正整数 ,在区间
,在区间 内,总存在
内,总存在 个数
个数 使得不等式
使得不等式 成立,求
成立,求 的最大值.
的最大值.
(本小题满分15分)已知数列 的前
的前 项和
项和 满足:
满足: (
( 为常数,且
为常数,且 ).
).
(1)设 ,若数列
,若数列 为等比数列,求
为等比数列,求 的值;
的值;
(2)在满足条件(1)的情形下,设 ,数列
,数列 的前
的前 项和为
项和为 ,若不等式
,若不等式 对任意的
对任意的 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
已知数列 的前
的前 项和为
项和为 ,且
,且 ,
, N*
N*
(1)求数列 的通项公式;
的通项公式;
(2)已知 (
( N*),记
N*),记
 (
(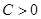 且
且 ),是否存在这样的常数
),是否存在这样的常数 ,使得数列
,使得数列 是常数列,若存在,求出
是常数列,若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(3)若数列 ,对于任意的正整数
,对于任意的正整数 ,均有
,均有 成立,求证:数列
成立,求证:数列 是等差数列;
是等差数列;
已知函数 ,若在定义域内存在
,若在定义域内存在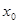 ,使得
,使得 成立,则称
成立,则称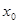 为函数
为函数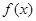 的局部对称点.
的局部对称点.
(1)若 、
、 R且
R且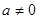 ,证明:函数
,证明:函数 必有局部对称点;
必有局部对称点;
(2)若函数 在区间
在区间 内有局部对称点,求实数
内有局部对称点,求实数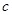 的取值范围;
的取值范围;
(3)若函数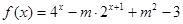 在R上有局部对称点,求实数
在R上有局部对称点,求实数 的取值范围.
的取值范围.
若在边长为 的正三角形
的正三角形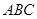 的边
的边 上有
上有 (
( N*,
N*, )等分点,沿向量
)等分点,沿向量 的方向依次为
的方向依次为 ,记
,记 ,若给出四个数值:①
,若给出四个数值:① ②
② ③
③ ④
④ ,则
,则 的值不可能的共有( )
的值不可能的共有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
已知函数 (其中
(其中 是自然对数的底数),
是自然对数的底数), ,
, .
.
(1)记函数 ,且
,且 ,求
,求 的单调增区间;
的单调增区间;
(2)若对任意
 ,
, ,均有
,均有 成立,求实数
成立,求实数 的取值范围.
的取值范围.
如图,在平面直角坐标系 中,已知椭圆
中,已知椭圆 :
: ,设
,设 是椭圆
是椭圆 上的任一点,从原点
上的任一点,从原点 向圆
向圆 :
: 作两条切线,分别交椭圆于点
作两条切线,分别交椭圆于点 ,
, .
.
(1)若直线 ,
, 互相垂直,求圆
互相垂直,求圆 的方程;
的方程;
(2)若直线 ,
, 的斜率存在,并记为
的斜率存在,并记为 ,
, ,求证:
,求证: ;
;
(3)试问 是否为定值?若是,求出该值;若不是,说明理由.
是否为定值?若是,求出该值;若不是,说明理由.
(本小题满分10分)选修4-4:坐标系与参数方程
极坐标系的极点为直角坐标系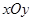 的原点,极轴为x轴的正半轴,两种坐标系中的长度单位相同. 已知曲线C的极坐标方程为
的原点,极轴为x轴的正半轴,两种坐标系中的长度单位相同. 已知曲线C的极坐标方程为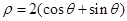 ,斜率为
,斜率为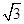 的直线
的直线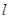 交y轴于点
交y轴于点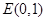 .
.
(1)求C的直角坐标方程,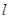 的参数方程;
的参数方程;
(2)直线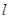 与曲线C交于A、B两点,求
与曲线C交于A、B两点,求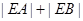 .
.
(本小题满分12分)已知函数 ,
, ,直线
,直线 与曲线
与曲线 切于点
切于点 且与曲线
且与曲线 切于点
切于点 .
.
(1)求a,b的值和直线 的方程;
的方程;
(2)证明: .
.
(本小题满分12分)已知点G是△ABC的重心,A(0,-1),B(0,1).在x轴上有一点M,满足 ,
, (若△ABC的顶点坐标为
(若△ABC的顶点坐标为 ,则该三角形的重心坐标为
,则该三角形的重心坐标为 .
.
(1)求点C的轨迹E的方程;
(2)若斜率为k的直线l与(1)中的曲线E交于不同的两点P、Q,且 ,试求斜率k的取值范围.
,试求斜率k的取值范围.