山东省青岛市高三上学期期末考试理科数学试卷
下列命题:
① 是方程
是方程 表示圆的充要条件;
表示圆的充要条件;
②把 的图象向右平移
的图象向右平移 单位,再保持纵坐标不变,横坐标变为原来的
单位,再保持纵坐标不变,横坐标变为原来的 ,得到函数
,得到函数 的图象;
的图象;
③函数 上为增函数;
上为增函数;
④椭圆 的焦距为2,则实数m的值等于5.
的焦距为2,则实数m的值等于5.
其中正确命题的序号为
| A.①③④ | B.②③④ | C.②④ | D.② |
若圆台两底面周长的比是1:4,过高的中点作平行于底面的平面,则圆台被分成两部分的体积比是
| A.1:16 | B.39:129 | C.13:129 | D.3:27 |
有3位同学参加测试,假设每位同学能通过测试的概率都是 ,且各人能否通过测试是相互独立的,则至少有一位同学能通过测试的概率为
,且各人能否通过测试是相互独立的,则至少有一位同学能通过测试的概率为
A. |
B. |
C. |
D. |
已知双曲线的方程为 ,双曲线的一个焦点到一条渐近线的距离为
,双曲线的一个焦点到一条渐近线的距离为 (c为双曲线的半焦距长),则双曲线的离心率e为__________.
(c为双曲线的半焦距长),则双曲线的离心率e为__________.
(本小题满分12分)
已知直线两直线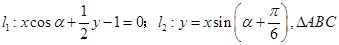 中,内角A,B,C对边分别为
中,内角A,B,C对边分别为 时,两直线恰好相互垂直;
时,两直线恰好相互垂直;
(I)求A值;
(II)求b和 的面积
的面积
(本小题满分12分)
右图为某校语言类专业N名毕业生的综合测评成绩(百分制)分布直方图,已知80~90分数段的学员数为21人
(I)求该专业毕业总人数N和90~95分数段内的人数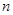 ;
;
(II)现欲将90~95分数段内的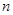 名毕业生分配往甲、乙、丙三所学校,若向学校甲分配两名毕业生,且其中至少有一名男生的概率为
名毕业生分配往甲、乙、丙三所学校,若向学校甲分配两名毕业生,且其中至少有一名男生的概率为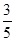 ,求
,求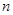 名毕业生中男女各几人(男女人数均至少两人)?
名毕业生中男女各几人(男女人数均至少两人)?
(III)在(II)的结论下,设随机变量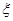 表示n名毕业生中分配往乙学校的三名学生中男生的人数,求
表示n名毕业生中分配往乙学校的三名学生中男生的人数,求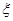 的分布列和数学期望.
的分布列和数学期望.
(本小题满分12分)
如图,ABCD为梯形, 平面ABCD,AB//CD,
平面ABCD,AB//CD,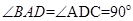
 ,E为BC中点,连结AE,交BD于O.
,E为BC中点,连结AE,交BD于O.
(I)平面 平面PAE
平面PAE
(II)求二面角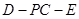 的大小(若非特殊角,求出其余弦即可)
的大小(若非特殊角,求出其余弦即可)
(本小题满分12分)
已知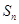 是等差数列
是等差数列 的前n项和,数列
的前n项和,数列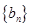 是等比数列,
是等比数列,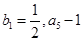 恰为
恰为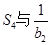 的等比中项,圆
的等比中项,圆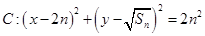 ,直线
,直线 ,对任意
,对任意 ,直线
,直线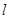 都与圆C相切.
都与圆C相切.
(I)求数列 的通项公式;
的通项公式;
(II)若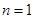 时,
时,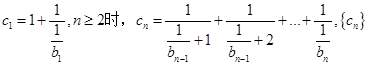 的前n项和为
的前n项和为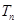 ,求证:对任意
,求证:对任意 ,都有
,都有
(本小题满分13分)
已知 处的切线为
处的切线为
(I)求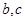 的值;
的值;
(II)若 的极值;
的极值;
(III)设 ,是否存在实数
,是否存在实数 (
(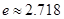 ,为自然常数)时,函数
,为自然常数)时,函数 的最小值为3.
的最小值为3.





 是纯虚数,则实数
是纯虚数,则实数 的值为
的值为



 和圆
和圆 的位置关系为
的位置关系为 ,则函数
,则函数 的大致图象为
的大致图象为



 的零点所在的大致区间是
的零点所在的大致区间是



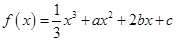 有两个极值点
有两个极值点 ,则直线
,则直线 的斜率的取值范围是
的斜率的取值范围是
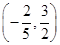


 的展开式中的常数项是_________.
的展开式中的常数项是_________. 时,函数
时,函数 的图像恒过点A,若点A在直线
的图像恒过点A,若点A在直线 上,则
上,则 的最小值为_________.
的最小值为_________. 所围成的图形的面积是_________.
所围成的图形的面积是_________. 的通项公式为
的通项公式为 ,试通过计算
,试通过计算 的值,推测出
的值,推测出 _________.
_________. 上一点
上一点 到其焦点F的距离为4;椭圆
到其焦点F的距离为4;椭圆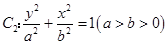 的离心率
的离心率 ,且过抛物线的焦点F.
,且过抛物线的焦点F. 和椭圆
和椭圆 的标准方程;
的标准方程; 交抛物线
交抛物线 轴于点N,已知
轴于点N,已知 ,求证:
,求证: 为定值.
为定值. 交椭圆
交椭圆 ,
,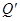 ,
, ,若点S满足:
,若点S满足: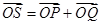 ,证明:点S在椭圆
,证明:点S在椭圆 粤公网安备 44130202000953号
粤公网安备 44130202000953号