（本小题满分12分）
右图为某校语言类专业N名毕业生的综合测评成绩（百分制）分布直方图，已知80~90分数段的学员数为21人
（I）求该专业毕业总人数N和90~95分数段内的人数
；
（II）现欲将90~95分数段内的名毕业生分配往甲、乙、丙三所学校，若向学校甲分配两名毕业生，且其中至少有一名男生的概率为
，求名毕业生中男女各几人（男女人数均至少两人）？
（III）在（II）的结论下，设随机变量
表示n名毕业生中分配往乙学校的三名学生中男生的人数，求的分布列和数学期望.
相关试题
（
）。
函数f(x)＝x3＋3ax2＋3bx＋c在x＝2处有极值，其图象在x＝1处的切线平行于直线3x＋y＋2＝0．
（１）求a，b的值； （２）求函数的极大值与极小值的差．
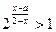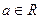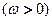的最小正周期为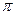
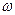的值；（2）求函数f(x)的单调递增区间；
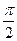]上的取值范围．
，
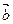=（1，2）．
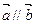，求tan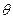
的值； （２）若
，
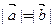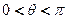，求相关知识点
推荐套卷
粤公网安备 44130202000953号