已知函数
(1) 时,求 在点 处的切线方程;
(2) 有 个零点, 且 .
(i)求 的取值范围;
(ii)证明 .
已知数列 是等差数列, 是等比数列, .
(1)求 , 的通项公式;
(2) , ,有 ,
(i)求证:对任意实数 ,均有 ;
(ii)求 所有元素之和.
已知椭圆 的左焦点为 ,右顶点为 , 为 上一点,且直线 的斜率为 , 的面积为 ,离心率为 .
(1)求椭圆的方程;
(2)过点 的直线与椭圆有唯一交点 (异于点 ),求证: 平分 .
正方体 的棱长为 , 分别为 中点, .
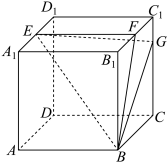
(1)求证: 平面 ;
(2)求平面 与平面 夹角的余弦值;
(3)求三棱锥 的体积.
在 中,角 的对边分别为 .已知 , , .
(1)求 的值;
(2)求 的值;
(3)求 的值.
中, 为AB边中点, ,则 ______(用 , 表示),若 , ,则 _______.
小桐操场跑圈,一周2次,一次5圈或6圈.第一次跑5圈或6圈的概率均为 ,若第一次跑5圈,则第二次跑5圈的概率为 ,6圈的概率为 ;若第一次跑6圈,则第二次跑5圈的概率为 ,6圈的概率为 .小桐一周跑11圈的概率为________;若一周至少跑11圈为动量达标,则连续跑4周,记合格周数为 ,则期望 _______.
,与 轴交于点 ,与 轴交于点 ,与 交于 、 两点, ,则 _________.
双曲线 的左、右焦点分别为 ,以右焦点 为焦点的抛物线 与双曲线交于第一象限的点P,若 ,则双曲线的离心率 ( )
| A. |
|
B. |
|
C. |
|
D. |
|
,在 上单调递增,且 为它的一条对称轴, 是它的一个对称中心,当 时, 的最小值为( )
| A. |
|
B. |
|
C. |
|
D. |
|