已知 、 ,则" "是" "的( )
| A. |
充分非必要条件 |
B. |
必要非充分条件 |
C. |
充要条件 |
D. |
既非充分又非必要条件 |
已知集合 , ,存在正数 ,使得对任意 ,都有 ,则 的值是________.
在椭圆 上任意一点 , 与 关于 轴对称,若有 ,则 与 的夹角范围为________.
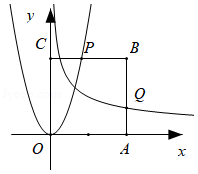
如图,已知正方形 ,其中 ,函数 交 于点 ,函数 交 于点 ,当 最小时,则 的值为________.
首届中国国际进口博览会在上海举行,某高校拟派4人参加连续5天的志愿者活动,其中甲连续参加2天,其他人各参加1天,则不同的安排方法有________种(结果用数值表示)