(本大题13分)如图,椭圆 的左焦点为
的左焦点为 ,过点
,过点 的直线交椭圆于
的直线交椭圆于 两点.
两点. 的最大值是
的最大值是 ,
, 的最小值是
的最小值是 ,满足
,满足 .
.
(1)求该椭圆的离心率;
(2)设线段 的中点为
的中点为 ,
, 的垂直平分线与
的垂直平分线与 轴和
轴和 轴分别交于
轴分别交于 两点,
两点, 是坐标原点.记
是坐标原点.记 的面积为
的面积为 ,
, 的面积为
的面积为 ,求
,求 的取值范围.
的取值范围.
已知:矩形 的两条对角线相交于点
的两条对角线相交于点 ,
, 边所在直线的方程为:
边所在直线的方程为:  ,点
,点 在
在 边所在直线上.
边所在直线上.
(1)求矩形 外接圆
外接圆 的方程。
的方程。
(2) 是圆
是圆 的内接三角形,其重心
的内接三角形,其重心 的坐标是
的坐标是 ,求直线
,求直线 的方程 .
的方程 .
(本小题满分14分)已知椭圆
 的左、右焦点分别为
的左、右焦点分别为 、
、 ,离心率为
,离心率为 ,且经过点
,且经过点 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)动直线 与椭圆
与椭圆 相切,点
相切,点 是直线
是直线 上的两点,且
上的两点,且 . 求四边形
. 求四边形 面积;
面积;
(Ⅲ)过椭圆 内一点
内一点 作两条直线分别交椭圆
作两条直线分别交椭圆 于点
于点 和
和 ,设直线
,设直线 与
与 的斜率分别为
的斜率分别为 、
、 ,若
,若 ,试问
,试问 是否为定值,若是,求出此定值;若不是,说明理由.
是否为定值,若是,求出此定值;若不是,说明理由.
(本小题满分14分)椭圆 过点
过点 ,离心率为
,离心率为 ,左右焦点分别为
,左右焦点分别为 ,过点
,过点 的直线交椭圆于
的直线交椭圆于 两点。
两点。
(1)求椭圆 的方程;
的方程;
(2)当 的面积为
的面积为 时,求
时,求 的方程.
的方程.
(本小题满分12分)某批发市场对某种商品的日销售量(单位:吨)进行统计,最近50天的统计结果如下:
| 日销售量 |
1 |
1.5 |
2 |
| 天数 |
10 |
25 |
15 |
| 频率 |
0.2 |
a |
b |
若以上表中频率作为概率,且每天的销售量相互独立.
(Ⅰ)求5天中该种商品恰好有两天的销售量为1.5吨的概率;
(Ⅱ)已知每吨该商品的销售利润为2千元,X表示该种商品某两天销售利润的和(单位:千元),求X的分布列和数学期望.
(本小题满分16分)设函数f(x)=xsinx(x∈R),
(Ⅰ)证明f(x+2kπ)-f(x)=2kπsinx,其中k为整数;
(Ⅱ)设x0为f(x)的一个极值点,证明  ;
;
(提示 )
)
(Ⅲ)设f(x)在(0,+∞)内的全部极值点按从小到大的顺序排列a1,a2, ,an, ,证明 .
.
设 和
和 是函数
是函数 的两个极值点,其中
的两个极值点,其中 ,
, .
.
(1)若曲线 在点
在点 处的切线垂直于
处的切线垂直于 轴,求实数
轴,求实数 的值;
的值;
(2)求 的取值范围;
的取值范围;
(3)若 ,求
,求 的最大值(
的最大值( 是自然对数的底数).
是自然对数的底数).
函数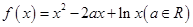 .
.
(1)函数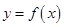 在点
在点 处的切线与直线
处的切线与直线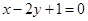 垂直,求a的值;
垂直,求a的值;
(2)讨论函数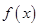 的单调性;
的单调性;
(3)不等式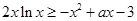 在区间
在区间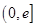 上恒成立,求实数a的取值范围.
上恒成立,求实数a的取值范围.
【原创】已知函数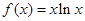 ,
,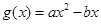 (a、b为常数).
(a、b为常数).
(1)求函数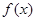 在点(1,
在点(1, )处的切线方程;
)处的切线方程;
(2)当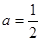 时,设
时,设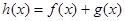 ,若函数
,若函数 在区间
在区间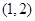 上存在极值点,求实数b的取值范围;
上存在极值点,求实数b的取值范围;
(本小题满分10分)在平面直角坐标系xOy中,椭圆C: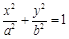 (a>b>0)的上顶点到焦点的距离为2,离心率为
(a>b>0)的上顶点到焦点的距离为2,离心率为 .
.
(1)求a,b的值.
(2)设P是椭圆C长轴上的一个动点,过点P作斜率为k的直线l交椭圆C于A、B两点.
(ⅰ)若k=1,求△OAB面积的最大值;
(ⅱ)若PA2+PB2的值与点P的位置无关,求k的值.
(本小题满分12分)已知椭圆 ,其中
,其中 是椭圆的右焦点,焦距为2,直线
是椭圆的右焦点,焦距为2,直线 与椭圆
与椭圆 交于点
交于点 ,点
,点 的中点横坐标为
的中点横坐标为 ,且
,且 (其中
(其中 ).
).
(1)求椭圆 的标准方程;
的标准方程;
(2)求实数 的值.
的值.
【改编】设函数 ,
,
(Ⅰ)若 时,求曲线
时,求曲线 单调区间;
单调区间;
(Ⅱ)当 时,
时, ,求实数
,求实数 的取值范围.
的取值范围.
(本小题14分)如图,已知某椭圆的焦点是 ,过点
,过点 并垂直于x轴的直线与椭圆的一个交点为B,且
并垂直于x轴的直线与椭圆的一个交点为B,且 ,椭圆上不同的两点
,椭圆上不同的两点 满足条件:
满足条件: 、
、 、
、 成等差数列.
成等差数列.
(1)求该椭圆的方程;
(2)求弦AC中点的横坐标;
(3)设弦AC的垂直平分线的方程为 ,求m的取值范围.
,求m的取值范围.
已知数列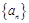 的前n项和为
的前n项和为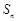 ,设数列
,设数列 满足
满足 .
.
(1)若数列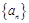 为等差数列,且
为等差数列,且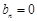 ,求数列
,求数列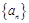 的通项公式;
的通项公式;
(2)若 ,
,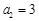 ,且数列
,且数列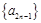 ,
,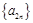 都是以2为公比的等比数列,求满足不等式
都是以2为公比的等比数列,求满足不等式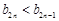 的所有正整数n的集合.
的所有正整数n的集合.
(本小题满分14分)已知函数 (
( 为自然对数的底数),曲线
为自然对数的底数),曲线 在
在 处的切线与直线
处的切线与直线 互相垂直.
互相垂直.
(Ⅰ)求实数 的值;
的值;
(Ⅱ)若对任意 ,
,  恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(Ⅲ)设 ,
,
 .问:是否存在正常数
.问:是否存在正常数 ,对任意给定的正整数
,对任意给定的正整数 ,都有
,都有 成立?若存在,求
成立?若存在,求 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由.