河南省商丘市高三第一次模拟考试理科数学试卷
已知集合A={x|0<x<2},B={x||x|>1},则A∩B=( ).
| A.(0,1) |
| B.(1,2) |
| C.(-∞,-1)∪(0,+∞) |
| D.(-∞,-1)∪(1,+∞) |
已知命题p: ∈R,x-2>lgx,命题q:
∈R,x-2>lgx,命题q: ∈R,
∈R,  >0,则( ).
>0,则( ).
| A.命题p∨q是假命题 |
| B.命题p∧q是真命题 |
C.命题p∨( )是假命题 )是假命题 |
D.命题p∧( )是真命题 )是真命题 |
已知向量a,b满足|a|=1,a⊥b,则向量a-2b在向量a方向上的投影为( ).
| A.1 | B. |
C.-1 | D. |
已知锐角α的终边上一点P(sin40°,1+cos40°),则α等于( ).
| A.10° | B.20° | C.70° | D.80° |
若某程序框图如图所示,则该程序运行后输出的B等于( ). 
| A.63 | B.31 | C.127 | D.15 |
已知抛物线 =4x与双曲线
=4x与双曲线 (a>0,b>0)有相同的焦点F,点A,B是两曲线的交点,若(
(a>0,b>0)有相同的焦点F,点A,B是两曲线的交点,若( +
+ )·
)· =0,则双曲线的离心率为( ).
=0,则双曲线的离心率为( ).
A. +2 +2 |
B. +1 +1 |
C. +1 +1 |
D. +1 +1 |
已知三棱锥的三视图如图所示,则它的外接球的表面积为( ). 
| A.4π | B.8π |
| C.12π | D.16π |
等比数列{ }的前n项和为
}的前n项和为 ,
, =4(a1+a3+ +
=4(a1+a3+ + ),a1a2a3=27,则a6=( ).
),a1a2a3=27,则a6=( ).
| A.27 | B.8l | C.243 | D.729 |
给出下列四个结论:
①若a,b∈[0,1],则不等式 ≤1成立的概率为
≤1成立的概率为 ;
;
②由曲线y= 与y=
与y= 所围成的封闭图形的面积为0.5;
所围成的封闭图形的面积为0.5;
③已知随机变量ξ服从正态分布N(3, ),若P(ξ≤5)=m,则P(ξ≤1)=1-m;
),若P(ξ≤5)=m,则P(ξ≤1)=1-m;
④ 的展开式中常数项为
的展开式中常数项为 .
.
其中正确结论的个数为( ).
| A.1 | B.2 | C.3 | D.4 |
已知函数f(x)满足f(x)=f( ),当x∈[1,3]时,f(x)=lnx,若在区间[
),当x∈[1,3]时,f(x)=lnx,若在区间[ ,3]内,曲线g(x)=f(x)-ax与x轴有三个不同的交点,则实数a的取值范围是( ).
,3]内,曲线g(x)=f(x)-ax与x轴有三个不同的交点,则实数a的取值范围是( ).
A.(0, ) ) |
B.(0, ) ) |
C.[ , , ) ) |
D.[ , , ) ) |
某同学有同样的画册2本,同样的集邮册3本,从中取出4本赠送给4位朋友,每位朋友1本,则不同的赠送方法共有_______种.
若圆C: +2x-4y+3=0关于直线2ax+by+6=0对称,则由点(a,b)向圆所作的切线长的最小值是_____________。
+2x-4y+3=0关于直线2ax+by+6=0对称,则由点(a,b)向圆所作的切线长的最小值是_____________。
已知函数y=f(x-1)+ 是定义在R上的奇函数,且f(0)=-1,若g(x)=1-f(x+1),则g(-3)=______________
是定义在R上的奇函数,且f(0)=-1,若g(x)=1-f(x+1),则g(-3)=______________
已知数列{ }通项公式为
}通项公式为 =-n+p,数列{
=-n+p,数列{ }通项公式为
}通项公式为 =
= ,设
,设 =
= 若在数列{
若在数列{ }中,
}中, >
> (n∈N﹡,n≠8),则实数p的取值范围是_______.
(n∈N﹡,n≠8),则实数p的取值范围是_______.
(本小题满分12分)在△ABC中,角A,B,C的对边分别为a,b,c,且sinA+sinB=2sinC,a=2b.
(Ⅰ)证明:△ABC是钝角三角形;
(Ⅱ)若 ,求c的值.
,求c的值.
(本小题满分12分)某批发市场对某种商品的日销售量(单位:吨)进行统计,最近50天的统计结果如下:
| 日销售量 |
1 |
1.5 |
2 |
| 天数 |
10 |
25 |
15 |
| 频率 |
0.2 |
a |
b |
若以上表中频率作为概率,且每天的销售量相互独立.
(Ⅰ)求5天中该种商品恰好有两天的销售量为1.5吨的概率;
(Ⅱ)已知每吨该商品的销售利润为2千元,X表示该种商品某两天销售利润的和(单位:千元),求X的分布列和数学期望.
(本小题满分12分)如图,在三棱柱ABC-A1B1C1中,已知AB⊥侧面BB1C1C,AB=BC=1,BB1=2,∠BCC1=60°。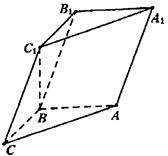
(Ⅰ)求证:C1B⊥平面ABC;
(Ⅱ)设 =λ
=λ (0≤A≤1),且平面AB1E与BB1E所成的锐二面角的大小为30°,试求λ的值.
(0≤A≤1),且平面AB1E与BB1E所成的锐二面角的大小为30°,试求λ的值.
(本小题满分12分)已知直线l的方程为y= x-2
x-2 ,又直线l过椭圆C:
,又直线l过椭圆C: (a>b>0)的右焦点,且椭圆的离心率为
(a>b>0)的右焦点,且椭圆的离心率为 .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点D(0,1)的直线与椭圆C交于点A,B,求△AOB的面积的最大值.
(本小题满分12分)已知函数f(x)=x+alnx在x=1处的切线l与直线x+2y=0垂直,函数g(x)=f(x)+ -bx.
-bx.
(Ⅰ)求实数a的值;
(Ⅱ)设x1,x2 (x1<x2)是函数g(x)的两个极值点,若b≥ ,求g(x1)-g(x2)的最小值.
,求g(x1)-g(x2)的最小值.
(本小题满分10分)选修4—1:几何证明选讲
如图,四边形ACED是圆内接四边形,AD、CE的延长线交于点B,且AD=DE,AB=2AC.
(Ⅰ)求证:BE=2AD;
(Ⅱ)当AC=2,BC=4时,求AD的长.
(本小题满分10分)选修4—4:坐标系与参数方程
已知直线l经过点P( ,1),倾斜角α=
,1),倾斜角α= ,圆C的极坐标方程为
,圆C的极坐标方程为 =
= cos(θ-
cos(θ- ).
).
(Ⅰ)写出直线l的参数方程,并把圆C的方程化为直角坐标方程;
(Ⅱ)设l与圆C相交于A,B两点,求点P到A,B两点的距离之积.



 则z=|x-3y|
则z=|x-3y| ,b∈(0,+∞),
,b∈(0,+∞), +
+ ≥|2x-1|-|x+1|恒成立,
≥|2x-1|-|x+1|恒成立, 粤公网安备 44130202000953号
粤公网安备 44130202000953号